Sort Them Out (1)

Sort Them Out (1)

Sort Them Out (1) printable sheet

 

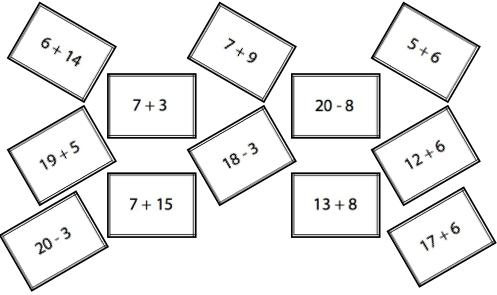
It's best to do this with $3$ other friends.

Share all the cards out equally among the four of you.

Work out what the answer is to each question on your cards.
Do you notice anything?
What do you notice?
Try sorting or arranging the cards in some way.

Why do this problem?

The intention of this problem is that children will work together as a team. It should help in developing mathematical language as well as providing interesting practice in addition and subtraction and possibly offer opportunities to share calculation strategies. It gives ample opportunities to practise calculations using numbers to $20$ and should support children to remember these facts so that they are able to recall and use them whenever they need to do so.

Possible approach

The sheet of cards will need to be printed out. Give out a set of cards to each group of four to six children - it is important to give out all the cards in the set! (The questions asked in the set do vary in difficulty so you may like to choose who to give specific cards to.) To begin with, give children time to work individually on the questions on their own cards. After a suitable period of time, encourage them to ask each other about the questions and answers on other cards. At this stage, members of the group can help each other with the questions, but discourage them from simply giving someone else an answer.

Key questions

Possible extension

Possible support

You can purposely give certain cards to certain children if you do not want to take them too far out of their comfort zone where calculation is concerned. It may be appropriate for some learners to share cards with someone who is slightly more confident with addition and subtraction than they are themselves. Encourage them both to feel responsible for their findings and ensure everyone is involved in the class discussion.