Skip over navigation
History of Trigonometry - Part 3
This is the third of three articles on the History of Trigonometry.
Part 2 (Sections 5 - 7) can be found here. Part 1 (Sections 1 - 4) can be found here.
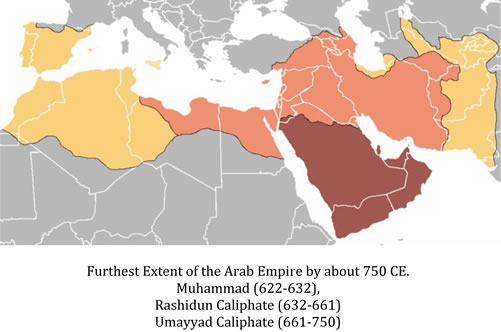
8. The Arabs collect knowledge from the known world
The Arab civilisation traditionally marks its beginning from the year 622 CE the date when Muhammad, threatened with assassination, fled from Mecca to Medina where Muhammad and his followers found safety and respect. Over a century later, the Arabs had established themselves as a powerful unified force across large parts of the Middle East and The Caliph Abu
Ja'far Al-Mansour moved from Damascus to establish the city of Baghdad during the years 762 to 766. Al-Mansour sent his emissaries to search for and collect knowledge. From China, they learnt how to produce paper, and using this new skill they started a programme of translation of texts on mathematics, astronomy, science and philosophy into Arabic. This work was continued by his successors,
Caliphs Mohammad Al-Mahdi and Haroun Al-Rasheed. The quest for knowledge became a lasting and significant part of Arab culture.
Al-Mansour had founded a scientific academy that became called 'The House of Wisdom'. This academy attracted scholars from many different countries and religions to Baghdad to work together and establish the traditions of Arabic science that were to continue well into the Middle Ages. Some of this work was later translated into Latin by Mediaeval scholars and passed on into Europe. The
dominance of Baghdad and the influence of the Arab World was to last for the next 500 years.
The scholars in the House of Wisdom came from many cultures and translated the works of Egyptian, Babylonian, Greek, Indian and Chinese astronomers and mathematicians. The Mathematical Treatise of Ptolemy was one of the first to be translated from the Greek into Arabic by Ishaq ben Hunayn (830-910). It was admired for its extensive content and became known
in Arabic as Al-Megiste (the Great Book). The name 'Almagest' has continued to this day and it is recognized as both the great synthesis and the culmination of mathematical astronomy of the ancient Greek world. It was translated into Arabic at least five times and constituted the basis of the mathematical astronomy carried out
in the Islamic world.
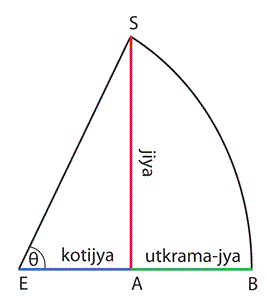
9. India: The Sine, Cosine and Versine
Greek astronomy began to be known in India during the period 300-400 CE. However, Indian astronomers had long been using planetary data and calculation methods from the Babylonians, and even though it was well after Ptolemy had written the Almagest, 4th century Indian astronomers did not entirely take over Greek planetary theory. Ancient works like the Panca-siddhantica (now lost) that had been transmitted through the version by Vrahamihira [See Part 1 section 3] and Aryabhata's Aryabhatiya (499 CE) demonstrated that Indian scholars had their own ways of dealing with astronomical problems and that they had great skill in
calculation.[See Note 1 below]
Even in the oldest Indian texts, the Chord [to remind yourself about Chords see the section on Claudius Ptolemy in the previous article] is not used, and instead there appear some very early versions of trigonometric tables using Sines. However, the Indian astronomers divided the $90^\circ$ arc into $24$ sections, thus obtaining values of
Sines for every $3^\circ45'$ of arc.
In this diagram, $SB$ is the arc for the angle $\theta$ and $AS$ is the jiya. So the relation between the jiya and our sine is:
$$ jiya (\theta)=R\sin\theta$$
where $R$ is the radius of the circle.
Many Indian Sine tables use $R = 3438$ which is the result if the circumference of the circle is $360 \times 60$ or $21,600$ minutes. [See Note 2 below]
By the 5th century, two other functions had been defined and used. The length $EA$ was called the kotijya (our cosine), and AB was called the utkrama-jya (our versine). This was sometimes called the sama meaning an 'arrow', or sagitta in Latin
The versine function for a circle radius $R$ is: $\mbox{vers }\theta = R - \cos\theta $ [See Note 3 below]
In Aryabhata's work, he uses $R = 3438$ and took this value to calculate his table of Sines. This became the standard for later works. Comparison with Varhamihira's Sines (in sexagesimal numbers) and Hipparchs' table (in lengths of chords) suggests a possible transmission of at least some of the Greek works to the Hindus. However, we have no way of knowing this for certain, and it is quite
possible that the Hindus calculated their values independently.
The 'Great Work' (the Mahabhaskariya) of Bhaskara I was written in about 600 CE. He produced a remarkable method for approximating values for the Sines, by using the ratio of two quadratic functions. This was based entirely on comparing the results of his calculations with earlier values. [See Note 4 below ]
However, since these tables only gave values for every $3^\circ 45'$, there was cnsiderable room for improvement. It is curious that since Ptolemy's table of chords enabled him to find values equivalent to Sines from $\frac{1}{4}^\circ$ to $90^\circ$ that the Indian scholars did not go further at this stage. Later, Brahmagupta (598-670) produced an ingenious method based on second order
differences to obtain the Sine of any angle from an initial set of only six values from $0^\circ$ in $15^\circ$ intervals to $90^\circ$.
10. Trigonometry in the Arab Civilisation
The introduction and development of trigonometry into an independent science in the Arab civilisation took, in all, some 400 years. In the early 770s Indian astronomical works reached the Caliph Al-Mansur in Baghdad, and were translated as the Zij al-Sindhind, and this introduced Indian calculation methods into
Islam.
Famous for his algebra book, Abu Ja'far Muhammad ibn Musa al-Khwarizmi (see The Development of Algebra Part 1) had also written a book on Indian methods of calculation (al-hisab al-hindi) and he produced an improved version of the Zij
al-Sindhind. Al-Khwarizmi's version of Zij used Sines and Versines, and developed procedures for tangents and cotangents to solve astronomical problems. Al-Khwarizmi's Zij was copied many times and versions of it were used for a long time.
Many works in Greek, Sanskrit, and Syriac were brought by scholars to Al-Mansur's House of Wisdom and translated. Among these were the works of Euclid, Archimedes Apollonius and of course, Ptolemy. The Arabs now had two competing versions of astronomy, and soon the Almagest prevailed.
The Indian use of the sine and its related functions were much easier to apply in calculations, and the sexagesimal system from the Babylonians continued to be used, so apart from these two changes, the early Arabic versions of the Almagest remained faithful to Ptolemy. [See Note 5 below]
Abu al-Wafa al-Buzjani (Abul Wafa 940-998) made important contributions to both geometry and arithmetic and was the first to study trigonometric identities systematically. The study of identities was important because by establishing relationships between sums and differences, and fractions and multiples of angles, more efficient astronomical calculations
could be conducted and more accurate tables could be established.
The sine, versine and cosine had been developed in the context of astronomical problems, whereas the tangent and cotangent were developed from the study of shadows of the gnomon. In his Almagest, Abul Wafa brought them together and established the relations between the six fundamental trigonometric functions for the first time. He also used $R = 1$ for the
radius of the basic circle.
From these relations Abul Wafa was able to demonstrate a number of new identities using these new functions:
$$sec^2\theta = 1 + tan^2\theta \mbox{. . . . . . . }cosec^2 \theta=1+cot^2 \theta$$
Abul Wafa also devised methods for calculating trigonometric tables by an improved differencing technique to obtain values that were accurate to $5$ sexagesimal ($8$ decimal) places.
Greek astronomers had long since introduced a model of the universe with the stars on the inside of a vast sphere. They had also worked with spherical triangles, but Abul Wafa was the first Arab astronomer to develop ways of measuring the distance between stars using his new system of trigonometric functions including the versine.
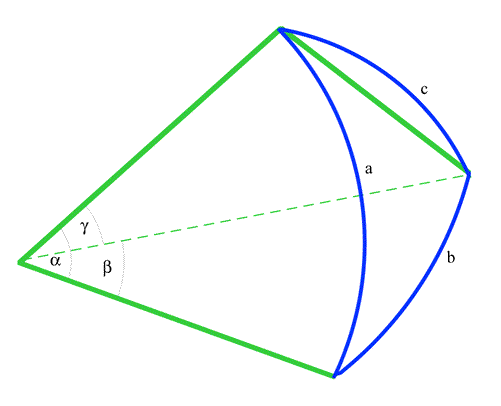
In the diagram above, the blue triangle with sides $a$, $b$, and $c$ represents the distances between stars on the inside of a sphere. The apex where the three angles $\alpha$, $\beta$, and $\gamma$ are marked, is the position of the observer. The blue curves are Great Circles on the sphere, and by measuring the angles, finding more accurate values for their functions, and assuming a value for $R$ the radius of the sphere, it became possible to find the great-circle distances between the stars.
By an ingenious application of Menelaos' Theorem [See History of Trigonometry Part 2] using special cases of great circles with two right angles, Abul Wafa showed how the theorem could be applied in spherical triangles. This was a considerable advance in Spherical Trigonometry that enabled the calculation of the correct direction for prayer
(the quibla) and was to have important applications in Navigation and Cartography.
The Abul Wafa crater of the Moon is named in recognition of his work in astronomy.
 |
Abu al-Rayhan Muhammad ibn Ahmad Al-Biruni (973-1050) was an outstanding scholar reputed to have written over 100 treatises on astronomy, science, mathematics, geography, history, geodesy and philosophy. Only about twenty of these works now survive, and only about a dozen of these have been published.
Al-Biruni's treatise entitled Maqalid 'ilm al-hay'a (Keys to the Science of Astronomy) ran to over one thousand pages and contained extensive developments in on trigonometry. Among many theorems, he produced a demonstration of the tangent formula, shown below.
|
From the diagram, $O$ is the centre of the semicircle, and $AED$ a right-angled triangle with a perpendicular from $E$ to $C$.
Consequently, triangles $AEC$ and $EDC$ are similar.
Angle $EOD$ is twice angle $EAD$, and angles $EAC$ and $DEC$ are equal.
If the radius of the circle $R =1$, then $EC = \sin \theta$ and $OC = \cos\theta$
$$\mbox{So }\tan\left(\frac{\theta}{2}\right)=\frac{EC}{AC}=\frac{\sin\theta}{1+\cos\theta} \mbox{ . . . and . . . } \tan\left(\frac{\theta}{2}\right)=\frac{DC}{EC}=\frac{1-\cos\theta}{\sin\theta}$$
From which he derived the half angle and multiple angle formulae. [See Note 6 below]
While many new aspects of trigonometry were being discovered, the chord, sine, versine and cosine were developed in the investigation of astronomical problems, and conceived of as properties of angles at the centre of the heavenly sphere. In contrast, tangent and cotangent properties were derived from the measurement of shadows of a gnomon and the problems of telling the time.
In his Demarcation of the Coordinates of Cities he used spherical triangles for finding the coordinates of cities and other places to establish local meridian (the quibla) and thereby finding the correct direction of Mecca, and in his Exhaustive Treatise on Shadows he showed how to use
gnomons [See A Brief History of Time Measurement] for finding the time of day.
Abu Muhammad Jabir ibn Aflah (Jabir ibn Aflah c1100 - c1160) probably worked in Seville during the first part of the 12th century. His work is seen as significant in passing on knowledge to Europe. Jabir ibn Aflah was considered a vigorous critic of Ptolemy's astronomy. His treatise helped to spread trigonometry in Europe in the 13th century, and his
theorems were used by the astronomers who compiled the influential Libro del Cuadrante Sennero (Book of the Sine Quadrant) under the patronage of King Alfonso X the Wise of Castille (1221-1284).
A result of this project was the creation of much more accurate astronomical tables for calculating the position of the Sun, Moon and Planets, relative to the fixed stars, called the Alfonsine Tables made in Toledo somewhere between 1252 and 1270. These were the tables Columbus used to sail to the New World, and they remained the most accurate tables until the 16th century.
By the end of the 10th century trigonometry occupied an important place in astronomy texts with chapters on sines and chords, shadows (tangents and cotangents) and the formulae for spherical calculations. There was also considerable interest in the resolution of plane triangles. But a completely new type of work by Nasir al-Din al-Tusi (Al-Tusi 1201-1274)
entitled Kashf al-qina 'an asrar shakl al-qatta (Treatise on the Secrets of the Sector Figure), was the first treatment of trigonometry in its own right, as a complete subject apart from Astronomy. The work contained a systematic discussion on the application of proportional reasoning to solving plane and spherical triangles, and a thorough treatment of the
formulae for solving triangles and trigonometric identities. Al-Tusi originally wrote in Persian, but later wrote an Arabic version. The only surviving Persian version of his work is in the Bodleian Library in Oxford.
This was a collection and major improvement on earlier knowledge. Books I, II and IV contain parts of the Elements, the Almagest and a number of other Greek sources. Book III deals with the basic geometry for spherical triangles and the resolution of plane triangles using the sine theorem:
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$$
Book V contains the principal chapters on trigonometry dealing with right-angled triangles and the six fundamental relations equivalent to those we use today; sine, cosine, tangent, cotangent, secant and cosecant. He provided many new proofs and showed how they could be used to solve many problems more easily.
 |
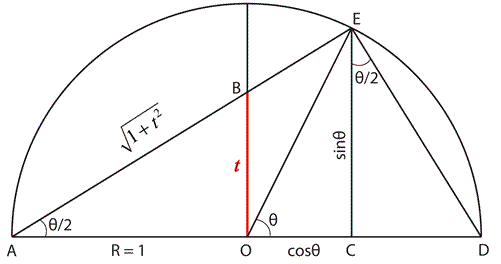
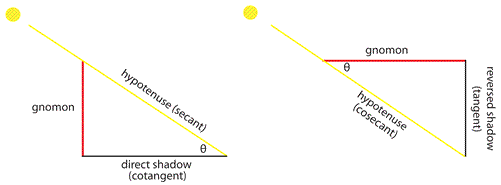
Al-Tusi invented a new geometrical technique now called the 'Al-Tusi couple' that generated linear motion from the sum of two circular motions. He used this technique to replace the equant used by Ptolemy, and this device was later used by Copernicus in his heliocentric model of the universe. |
| Al-Tusi was one of the greatest scientists of Mediaeval Islam and responsible for some 150 works ranging from astronomy, mathematics and science to philosophy and poetry. |
11. Arab Science and Technology Reaches Europe
The Arab astronomers had learnt much from India, and there was contact with the Chinese along the Silk Road and through the sea routes, so that Arab trading posts were established in India and in China. Through these contacts Indian Buddhism spread into China and was well established by the 3rd century BCE, probably later carrying with it some of the calculation techniques of Indian
astronomy. However few, if any, technological innovations seemed to have passed from China to India or Arabia.
By 790 CE, the Arab empire had reached its furthest expansion in Europe, conquering most of the Iberian peninsula, an area called Al-Andalus by the Arabs. [See Note 7 below]
At this time many religions and races coexisted in Iberia, each contributing to the culture. The Muslim religion was generally very tolerant towards others, and literacy in Islamic Iberia was more widespread than any other country in Western Europe. By the 10th century Cordoba was said to have equally good libraries and educational establishments as Baghdad, and the cities of Cordoba and
Toledo became centres of a flourishing translation business.
Between 1095 and 1291 a series of religiously inspired military Crusades were waged by the Christians of Europe against the Arab Empire. The principal reason was the restoration of Christian control over the Holy Land, but there were also many other political and economic reasons. [See Note 8 below]
In all this turmoil and conflict there were periods of calm and centres of stability, where scholars of all cultures were able to meet and knowledge was developed, translated and transmitted into Western Europe. The three principal routes through which Greek and Arab science became known were Constantinople (now Istanbul) Sicily and Spain. Greek texts became known to European monks and
scholars who travelled with the armies through Constantinople on their way South to the Holy Land. These people learnt Greek and were able to translate the classical works into Latin. From Sicily, Arabs traded with Italy, and translation took place there, but probably the major route by which Arabic science reached Europe was from the translation houses of Toledo and Cordoba, across the Pyrenees
into south-western France.
During the twelfth and thirteenth century hundreds of works from Arabic, Greek and Hebrew sources were translated into Latin and the new knowledge was gradually disseminated across Christian Europe.
Geometrical knowledge in early Mediaeval Europe was a very practical subject. It dealt with areas, heights, volumes and calculations with fractions for measuring fields and the building of large manors, churches, castles and cathedrals.
Hugh of St. Victor (1078-1141) in his Practica Geometriae divides the material into Theorica (what is known and practised by a teacher) and Practica (what is done by a builder or mason). Theoretical geometry in the Euclidean sense was virtually unknown until the first translations of Euclid appeared in the West.
The astrolabe was commonly used to measure heights by using its 'medicline' (a sighting instrument fixed at the centre of the circle) and the shadow square engraved in the centre of the instrument, and then comparing the similar triangles. The horizontal distance from the centre of the astrolabe to the edge of the square was marked with twelve equal divisions.
This system was in use well into the 16th century as seen in the illustration below:
This is from Thomas Digges' Pantometria of 1571. The same system is still used, but the square in the quadrant is marked with six divisions.
A popular twelfth century text, the Artis Cuiuslibet Consummatio shows the gradual insertion of more technical knowledge, where the measuring of heights (altimetry) was much more related to astronomy, showing how to construct gnomons and shadow squares. Gradually the translations made on the continent of Europe came to England.
Richard of Wallingford (1292-1336)
After entering Oxford University in about 1308, Richard entered monastic life at St Alban's in 1316. After his ordination as a priest, his Abbot sent him back to Oxford where he studied for nine years. In 1327 he became Abbot of St Albans.
 |
Richard's early work was a series of instructions (canons) for the use of astronomical tables that had been drawn up by John Maudith, the Merton College Astronomer. Later he wrote an important work, the Quadripartitum, on the fundamentals of trigonometry needed for the solution of problems of spherical astronomy. The first part of this work is a theory of trigonometrical identities, and was regarded as a basis for the calculation of sines, cosines, chords and versed sines. The next two parts of the Quadripartitum dealt with a systematic and rigorous exposition of Menelaos' theorem. The work ends with an application of these principles to astronomy. The main sources of the work appear to be Ptolemy's Almagest, and Thabit ibn Qurra (826-901 CE). |
The Quadripartitum was probably the first comprehensive mediaeval treatise on trigonometry to have been written in Europe, at least outside Spain and Islam. When Richard was abbot of St. Albans, he revised the work, taking into account the Flores of Jabir ibn Afla.
In 1326 to 1327 Richard also designed a calculation device, called an equatorium, a complex geared astrolabe with four faces. He described how this could be used to calculate lunar, solar and planetary longitudes and thereby predict eclipses in his Tractatus Albionis. It is possible that this led to his design for an
astronomical clock described in his Tractatus Horologii Asronomici, (Treatise on the Astronomical Clock) of 1327, which was the most complex clock mechanism known at the time. The mechanism comprised a rotating star map that modeled the lunar eclipse and planets by gearing, presented as a geocentric model. It appeared at a transitional period in clock design,
just before the advent of the escapement. This makes it one of the first true clocks, and certainly one of first self powered models of the heavens. Unfortunately it was destroyed during Henry VIII's reformation at the dissolution of St Albans Monastery in 1539.
Georg von Peuerbach (1423-1461)
Peuerbach's work helped to pave the way for the Copernican conception of the world system; he created a new theory of the planets, made better calculations for eclipses and movements of the planets and introduced the use of the sine into his trigonometry.
| His early work, Tabulae Eclipsium circulated in manuscript was not published until 1514, contained tables of his eclipse calculations that were based on the Alfonsine Tables. He calculated sines for every minute of arc for a radius of 600,000 units and he introduced the Hindu-Arabic numerals in his tables. [See Note 9 below] |  |
Peuerbach's Theoricae Novae Planetarum, (New Theories of the Planets) was composed about 1454 was published in 1473 by Regiomontanus' printing press in Nuremburg. While the book was involved in attempting a technical resolution of the theories of Eudoxus and Ptolemy, Peuerbach claimed that the movement of the planets was determined by the Sun, and this has
been seen as a step towards the Copernican theory. This book was read by Copernicus, Galileo and Kepler and became the standard astronomical text well into the seventeenth century.
In 1460 he began working on a new translation of Ptolemy's Almagest, but he had only completed six of the projected thirteen books before died in 1461.
Johannes Muller von Konigsberg or Regiomontanus (1436-1476)
 |
Regiomontanus had become a pupil of Peuerbach at the University of Vienna in 1450. Later, he undertook with Peuerbach to correct the errors found in the Alfonsine Tables. He had a printing press where he produced tables of sines and tangents and continued Puerbach's innovation of using Hindu-Arabic numerals. |
| As promised, he finished Peuerbach's Epitome of the Almagest, which he completed in 1462 and was printed in Venice. The Epitome was not just a translation, it added new observations, revised calculations and made critical comments about Ptolemy's work. |  |
Realising that there was a need for a systematic account of trigonometry, Regiomontanus began his major work, the De Triangulis Omnimodis (Concerning Triangles of Every Kind) 1464. In his preface to the Reader he says,
"For no one can bypass the science of triangles and reach a satisfying knowledge of the stars .... You, who wish to study great and wonderful things, who wonder about the movement of the stars, must read these theorems about triangles. Knowing these ideas will open the door to all of astronomy and to certain geometric problems. For although certain figures must be transformed into triangles to be solved, the remaining questions of astronomy require these books." [See Note 10 below]
The first book gives the basic definitions of quantity, ratio, equality, circles, arcs, chords and the sine function. Next come a list of axioms he will assume, and then $33$ theorems for right, isosceles and scalene triangles. The formula for the area of a triangle is given followed by the sine rule giving examples of its application. Books III to V cover the all-important theory of spherical trigonometry. The whole book is organised in the style of Euclid with propositions and theorems set out in a logical hierarchical manner. This work, published in 1533 was of great value to Copernicus.
Regiomontanus also built the first astronomical observatory in Germany at Nuremburg with a workshop where he built astronomical instruments. He also took observations on a comet in 1472 that were accurate enough to allow it to be identified as Halley's Comet that reappeared 210 years later.
Regiomontanus died during an outbreak of plague in Rome in 1476.
12. The Final Chapter: Trigonometry Changes the World System
Nicolaus Copernicus (1473 - 1543)
Copernicus wrote a brief outline of his proposed system called the Commentariolus that he circulated to friends somewhere between 1510 and 1514. By this time he had used observations of the planet Mercury and the Alfonsine Tables to convince himself that he could explain the motion of the Earth as one of the planets. The manuscript of Copernicus' work has survived and it is thought that by the 1530s most of his work had been completed, but he delayed publishing the book.
His student, Rheticus read the manuscript and made a summary of Copernicus' theory and published it as the Narratio Prima (the First Account) in 1540. Since it seemed that the Narratio had been well accepted by colleagues, Copernicus was persuaded to publish more of his main work, and in 1542 he published a section on his spherical trigonometry as De lateribus et angulis traingulorum (On the sides and angles of triangles). Further persuaded by Rheticus and others, he finally agreed to publish the whole work, De Revolutionibus Orbium Coelestium (The Revolutions of the Heavenly Spheres) and dedicated it to Pope Paul III. It appeared just before Copernicus' death in 1543. [See Note 11 below]
Georg Joachim von Lauchen called Rheticus (1514-1574)
 |
Rheticus had facilitated the publication of Copernicus' work, and had clearly understood the basic principles of the new planetary theory.
In 1551, with the help of six assistants, Rheticus recalculated and produced the Opus Palatinum de Triangulis (Canon of the Science of Triangles) which became the first publication of tables of all six trigonometric functions. This was intended to be an introduction to his greatest work, The Science of Triangles.
When he died his work was still unfinished, but like Copernicus, Rheticus acquired a student, Valentinus Otho who supervised the calculation (by hand) of some one hundred thousand ratios to at least ten decimal places filling some 1,500 pages. This was finally completed in 1596. These tables were accurate enough to be used as the basis for astronomical calculations up to the early 20th
century.
|
Bartholomaeus Pitiscus (1561 - 1613)
 |
The term trigonometry is due to Pitiscus and as first appeared in his Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus, published in 1595. A revised version in1600 was the Canon triangularum sive tabulae sinuum, tangentium et secantium ad partes radii 100000 (A Canon of triangles, or tables of sines tangents and secants with a radius of 100,000 parts.) The book shows how to construct sine and other tables, and presents a number of theorems on plane and spherical trigonometry with their proofs. [See Note 11 below] |
However, soon after Rheticus' Opus Palatinum was published, serious inaccuracies were found in the tangent and secant tables at the ends near $1^\circ$ and $90^\circ$. Pitiscus was commissioned to correct these errors and obtained a manuscript copy of Rheticus' work. Many of the results were recalculated and new pages were printed incorporating the corrections. Eventually, Pitiscus published a new work in 1613 incorporating that of Rheticus with a table of sines calculated to fifteen decimal places entitled the Thesaurus Mathematicus.
By the beginning of the seventeenth century, the science of trigonometry had become a sophisticated technique used in calculating more and more accurate tables for use in astronomy and navigation, and had been instrumental in fundamentally changing man's concept of his world.
Reflection
See the notes to this article to read some thoughts on the value of teachig the history of mathematics.
References
Aveni, A, (1997) Stairways to the Stars. N.Y and Chichester Wiley
Skywatching in three ancient cultures: Megalithic Astronomy, the Maya and the Inca. The first chapter (almost a third of the book) gives a delightful and straightforward explanation of how much we can discover with the naked eye.
With clear diagrams and explanations this give a fascinating insight into the less well-known aspects of these ancient cultures.
Van Brummelen, G. (2009) The Mathematics of the Heavens and the Earth: The Early History of Trigonometry. Princeton, Princeton University Press.
This is the first major history in English of the early development of trigonometry. Glen van Brummelen's extensive research shows how the earliest activities in Egypt and Babylon led to the mathematical work of the Hindus and the Greeks that was developed by the Arabs over some 400 years into a sophisticated science separate from astronomy before it was passed on to Western European
astronomers and mathematicians.
Evans, J. (1998) The History and Practice of Ancient Astronomy. Oxford.O.U.P.
Beginning from about 700 BCE this book examines in detail both the practical and theoretical astronomy developed by the Egyptians, Babylonians and Greeks, up to the 16th century with the final resolution of the planetary system with Copernicus and Kepler.
Hughes, B. (1967) Regiomontanus on Triangles. London, University of Wisconsin Press
This is a translation with an introduction and notes, of the work completed in 1464, but published posthumously in 1533 of De triangulis omnimodis (On triangles of every kind) by Johan Muller, known as Regiomontanus. In this first edition, reproductions of the original Latin pages face the English translations. The book was written principally as a
contribution to the science of astronomy, but we now recognise Regiomontanus as the first European scholar who treated trigonometry as a theoretical science, setting out a series of logical propositions and proofs in the style of Euclid.
Maor E. (1998) Trigonometric Delights. Princeton, Princeton University Press.
Eli Maor presents a selection of the main elements of trigonometry and an account of its vital contribution to astronomy, science and social development. Interesting mathematical episodes to suit pupils at all levels, with notes and references for further exploration.
Rashed, R. (1996) (Ed.) Encyclopaedia of the History of Arabic Science. Vol 2.
This volume includes numeration and arithmetic, algebra, geometry and trigonometry. London. Routledge.
Victor, S.K. (1979) Practical Geometry in the High Middle Ages: Artis Cuiuslibet Consummatio and the Practike de Geometrie.
This is a translation and critical edition of these two major Mediaeval works. Philadelphia. American Philosophical Society
Bender, D. (1998) "A proposal for the striking mechanism on the Wallingford Clock." Antiquarian Horology 24, 2 1998a (134-140).
"A proposal for the eclipse mechanism for the Wallingford Clock." Antiquarian Horology 24, 3 1998b (217-224)
A fascinating description of one person's 'detective quest' to understand Richard of Wallingford's description of the workings of his amazing device.
Web Links
The Mactutor website for biographies of mathematicians and a special section on Trigonometry http://www-history.mcs.st-and.ac.uk/history/
The Muslim Heritage Site is very interesting. It is a valuable source of information on "1,000 years of missing history from 600 to 1600." You can find a large number of biographies of Muslim Scholars of the Past, a time Line of Events, and much more. http://www.muslimheritage.com
The Wallingford Clock http://www.wallingfordclock.talktalk.net Here is the general description and explanation of the various mechanisms of the reconstruction of the clock. Some parts of this site may not work.
There are many specialised websites where you can obtain information. If you 'Google' your enquiry and use the Wikipedia option you can usually obtain reasonably reliable results and ideas for more searches if you need to look any further.
Notes
1. See Part 1 section 3 on the Sulbasutras.
2. See Note 4 in Part1.
The use of the capital S in Sine is to show that the radius of the circle used is not unity, or the same as $\sin\theta$ in our system, but could be an arbitrary length R. This means that Sin$\theta$ is equal to R sin$\theta$ . In the Indian texts, different astronomers took different values for R, and in most cases the value had to be deduced from the context.
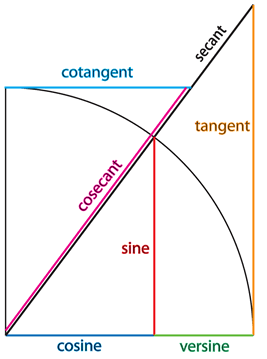
3. The advantage of the 'versine' (or reversed sine) is that it's value is always positive and so its logarithm is defined everywhere (except at $0^\circ$ and $180^\circ$). A positive logarithm was necessary when calculations had to be done using tables. The most important use was in navigation, for calculating the distance between two points on a sphere. The perpendicular distance from the mid point of a chord to a curve is still used as a measure of 'deviation from straightness', for example, by railway engineers. It is used also in optics for measuring the curvature of lenses and mirrors, where he versine is sometimes called the sagitta from the Latin for arrow.
4. Compare the sine curve from $0^\circ$ to $180^\circ$ with $y = -a(x- \pi/2)^2 + c$. By adjusting the values of $a$ and $c$, it is possible to produce a curve of 'best fit' inside the sine curve. You can obtain a remarkably good fit for $0 < x < \pi$.
5. The Hindu word jiya for the sine was adopted by the Arabs who called the sine jiba. Eventually jiba became jaib and this word actually meant a 'fold'. When Europeans translated the Arabic works into Latin they translated jaib into the word sinus meaning a fold in Latin. In his Practica Geometriae (1220) Fibonacci uses the term sinus rectus arcus which soon encouraged the universal use of the word sine.
6. In the diagram, if $OB = t$ and $R = 1$, then in triangle $ABO, AO^2 + OB^2 = 1 + t ^2$. From which we get the familiar parametric formulae.
$$\cos\theta=\frac{1-t^2}{1+t^2}\mbox{ etc.}$$
7. The maximum area occupied by the Arabs was most of Spain and Portugal with the exception of the kingdom of Asturias in the North, and a part of France now called the Languedoc.
8. The Holy Land with its capital Jerusalem, consisted roughly of what is now Israel and Palestine. There were many other reasons for the Crusades; the loss of power and territory of the older Christian Empires, the growing problem of the slave trade run by Arabs, and by taking part in these campaigns, some Christian kingdoms thought they could gain political advantage over their
rivals.
9. The reason for using such large numbers for the radius is much the same as in the past, the arithmetic was much easier using a large unit like 100,000 where the small parts (in this case minutes of arc) could be managed in integral parts rather than fractions. Similar considerations were applied by Napier, Briggs and Burgi in their invention of logarithms.
10. This quotation comes from the preface to the reader in De Triangulis, translated by Barnabas Hughes.
11. You can see Copernicus' book on Wikipedia at: http://en.wikipedia.org/wiki/De_revolutionibus_orbium_coelestium
You may also like
Divided Differences
When in 1821 Charles Babbage invented the `Difference Engine' it was intended to take over the work of making mathematical tables by the techniques described in this article.