Skip over navigation
Take a long (at least 200cm) piece of narrow paper:
Fold it in half by taking the right end over to the left (the pictures show it slightly opened just to make it clearer):
Fold it in half again, right over left:
and again:
Paper Curves
Age 7 to 11
Challenge Level 
Paper Curves
Take a long (at least 200cm) piece of narrow paper:
Fold it in half by taking the right end over to the left (the pictures show it slightly opened just to make it clearer):
Fold it in half again, right over left:
and again:
(It may be that you always prefer to fold left over to the right - that's ok, as long as you are always doing the same!)
THEN
1. Keep on folding into halves as many times as you can.
2. Press VERY hard onto the fold to make good creases.
3. Open out the paper so that it stands up on edge like in the pictures and make each fold a right angle (re-creasing may be necessary, but do not reverse the fold).
4. Stand a long way above and look down at what you can see!
5. Discuss with others what you notice.
Why do this problem?
This problem offers a novel way of exploring connections between Mathematics and Art. It is important for learners to have plenty of opportunity to discuss with others and to verify ideas.
Possible approach
Some groups of children may need a demonstration by an adult, particularly to ensure good folding and creasing as you work through the instructions given. Encouraging them to work in pairs will mean they can help each other produce the folds and they also have someone with whom to talk.
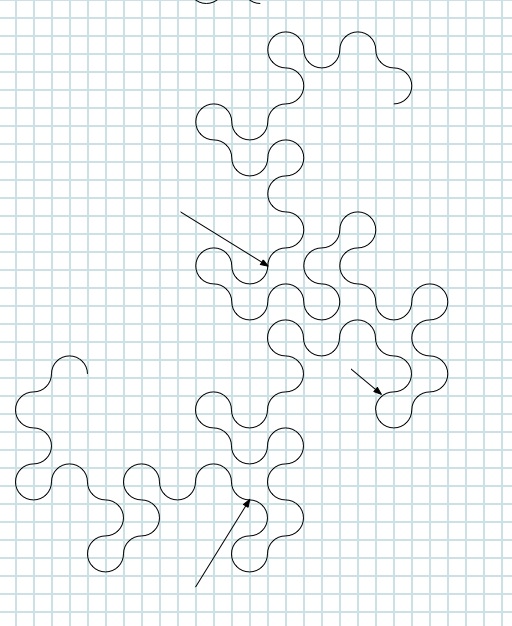
(For checking purposes, this image shows the progression in folds from the third to the eighth.)
In fact, this series of folds produces what is known as a 'dragon curve'. It will be interesting to see whether any children observe the dragon shape. They are likely to be fascinated and amused by the fact that it has been investigated by several mathematicians!
Key questions
What do you see?
Does it look like anything?
What could you try now?
Possible extension
Try slightly different alternatives like folding right over left and then left over right etc. Ask pupils to predict whether the result will be the same or different and why.
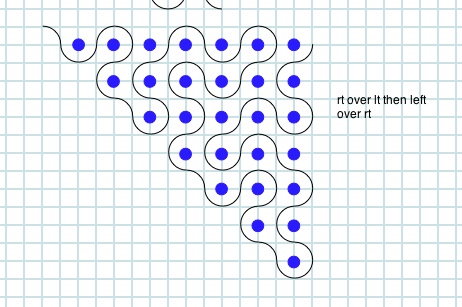
Drawing on a computer may be enhanced by producing a curved turn rather a right angle. Five folds using right over left then left over right produced the following:
Some pupils may like to go further by looking at the successive mid-points:
Possible support
Some pupils may require adult help with the manipulative skills of folding and creasing.
You may also like
Sponge Sections
You have been given three shapes made out of sponge: a sphere, a cylinder and a cone. Your challenge is to find out how to cut them to make different shapes for printing.
Plaiting and Braiding
This article for students gives some instructions about how to make some different braids.
Celtic Knotwork Patterns
This article for pupils gives an introduction to Celtic knotwork patterns and a feel for how you can draw them.