Skip over navigation
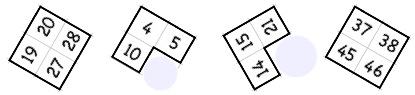
Complete each jigsaw and then put the pieces into the outline squares, which can be printed from here.pdf.
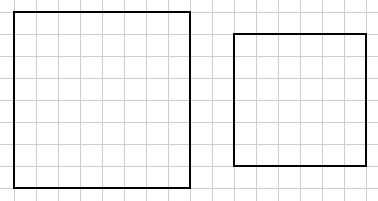
2. Place the smaller square of numbers on top of the other larger square in any way you like so that the small centimetre squares match up. (You may find it easier to copy the numbers on the smaller square onto a transparent sheet.)
3. Explore what happens when you add together the numbers that appear one on top of the other.
4. In your group, explore any other ideas that you come up with.
When you've looked at the thirty six combinations then you probably need to ask, "I wonder what would happen if we ...?". Change one small thing, explore that and then compare your two sets of results.
You might like to ask, "Why ...?".
Sorting the Numbers
Age 5 to 11
Challenge Level 
Well how about doing a simple jigsaw ?
This problem has been designed to be worked on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Notes.
1. There are two jigsaw puzzles that your teacher can print out for you from here.pdf.
Complete each jigsaw and then put the pieces into the outline squares, which can be printed from here.pdf.
2. Place the smaller square of numbers on top of the other larger square in any way you like so that the small centimetre squares match up. (You may find it easier to copy the numbers on the smaller square onto a transparent sheet.)
3. Explore what happens when you add together the numbers that appear one on top of the other.
4. In your group, explore any other ideas that you come up with.
When you've looked at the thirty six combinations then you probably need to ask, "I wonder what would happen if we ...?". Change one small thing, explore that and then compare your two sets of results.
You might like to ask, "Why ...?".
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.