Skip over navigation
Steve said the following
I sketched four vertical asymptotes and a sketch showed that a function which decayed to zero from above at $x \rightarrow \pm \infty$ could have the right sorts of properties.
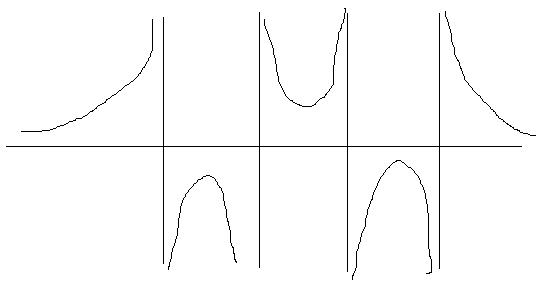
To get the right asymptotes and behaviour at $\pm \infty$ I guessed the following curve, choosing to make it symmetric about the origin for simplicity
$$
y = \frac{1}{(x-2)(x-1)(x+1)(x+2)}
$$
This worked: it has a turning point at $x$ between $-2$ and $-1$ another turning point at $x$ between $1$ and $2$ and a turning point at $x=0$.
The plot of this from graphmatica is as follows
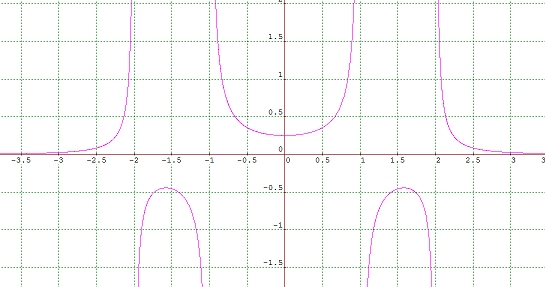
It seems likely that many such curves, with differing constants, would also give the correct behaviour. To see why, upon differentiation, I get a cubic polynomial divided by another polynomial. For zeros the numerator would need to be zero and a cubic can have three real roots. I could choose the constants to have the correct number of real roots.
I then considered the second request. Initially, I thought that this seemed impossible, but then started to work through the possibilities for asymptotes. By turning the middle turning point into a point of inflection I would have a graph with the correct behaviour.
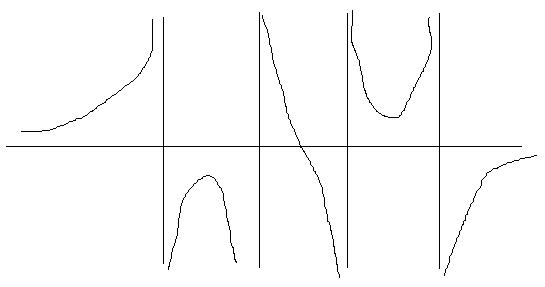
I wondered how to convert the behaviour of the central turning point and decided that the curve needed to be forced to pass through the origin and also to be antisymmetric. I therefore multiplied the expression by $x$, realising that this wouldn't affect the 'topological' behaviour at the other turning points. A plot of the curve
$$
y = \frac{x}{(x-2)(x-1)(x+1)(x+2)}
$$
gave graph
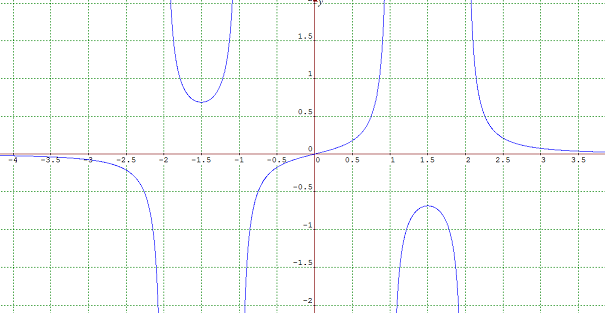
Which has the correct behaviour.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Rational Request
Age 16 to 18
Challenge Level 





- Problem
- Student Solutions
Steve said the following
I sketched four vertical asymptotes and a sketch showed that a function which decayed to zero from above at $x \rightarrow \pm \infty$ could have the right sorts of properties.

To get the right asymptotes and behaviour at $\pm \infty$ I guessed the following curve, choosing to make it symmetric about the origin for simplicity
$$
y = \frac{1}{(x-2)(x-1)(x+1)(x+2)}
$$
This worked: it has a turning point at $x$ between $-2$ and $-1$ another turning point at $x$ between $1$ and $2$ and a turning point at $x=0$.
The plot of this from graphmatica is as follows

It seems likely that many such curves, with differing constants, would also give the correct behaviour. To see why, upon differentiation, I get a cubic polynomial divided by another polynomial. For zeros the numerator would need to be zero and a cubic can have three real roots. I could choose the constants to have the correct number of real roots.
I then considered the second request. Initially, I thought that this seemed impossible, but then started to work through the possibilities for asymptotes. By turning the middle turning point into a point of inflection I would have a graph with the correct behaviour.

I wondered how to convert the behaviour of the central turning point and decided that the curve needed to be forced to pass through the origin and also to be antisymmetric. I therefore multiplied the expression by $x$, realising that this wouldn't affect the 'topological' behaviour at the other turning points. A plot of the curve
$$
y = \frac{x}{(x-2)(x-1)(x+1)(x+2)}
$$
gave graph

Which has the correct behaviour.
You may also like
Power Up
Show without recourse to any calculating aid that 7^{1/2} + 7^{1/3} + 7^{1/4} < 7 and 4^{1/2} + 4^{1/3} + 4^{1/4} > 4 . Sketch the graph of f(x) = x^{1/2} + x^{1/3} + x^{1/4} -x

