Skip over navigation
Mrs Bunting's class was playing a game using interlocking cubes. All the boys took a red cube and all the girls took a green cube.
Then the children took a black cube if they had dark coloured hair and a yellow cube if they had light coloured hair. They stuck their two cubes together.
The pairs of cubes looked like this:
The next day they did the same again except that this time, they had three cubes each. As well as a having a green or red and a yellow or black, they took a brown cube if they had brown eyes and a blue cube if they had blue eyes.
The Hair Colour Game
Age 7 to 11
Challenge Level 
Mrs Bunting's class was playing a game using interlocking cubes. All the boys took a red cube and all the girls took a green cube.
Then the children took a black cube if they had dark coloured hair and a yellow cube if they had light coloured hair. They stuck their two cubes together.
The pairs of cubes looked like this:
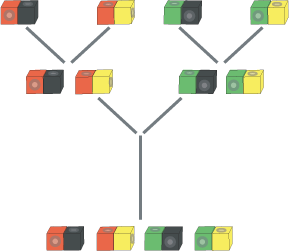
The children then got into four groups according to their pair
of cubes.
Can you explain what these pairs of cubes stand for?
Mrs Bunting showed them a way of recording the way they had
sorted themselves into different groups, called a tree
diagram.
At the bottom were all the pairs of cubes. Then they divided
into two branches. The red cubes went to the left and the green
cubes went to the right.
Then they divided into whether they had black cubes or yellow
cubes. Now there were four branches.
Here is the tree diagram:
The next day they did the same again except that this time, they had three cubes each. As well as a having a green or red and a yellow or black, they took a brown cube if they had brown eyes and a blue cube if they had blue eyes.
How many different groups were there then? Can you draw the
new tree diagram?
What happens if no one had dark hair and blue eyes? How could
you show that?
You may also like
Sponge Sections
You have been given three shapes made out of sponge: a sphere, a cylinder and a cone. Your challenge is to find out how to cut them to make different shapes for printing.
Plaiting and Braiding
This article for students gives some instructions about how to make some different braids.
Celtic Knotwork Patterns
This article for pupils gives an introduction to Celtic knotwork patterns and a feel for how you can draw them.