Skip over navigation


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
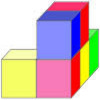
Solids
Age 11 to 16
Challenge Level 





- Problem
- Teachers' Resources
Why do this problem?
This task
encourages the development of team working skills such as
listening, asking questions, finding out what others think,
reflecting and making sense of what has been said, and eventually
coming to a consensus. If you wish to learn more about these skills
and find other team-building tasks look at this article.
In addition learners are
expected to use precision in describing an arrangement of
objects.
Possible approach
The task is based on a
team of four plus an observer.
You will need plenty of
cubes of any colour.
Explain the rules before
any equipment is handed out as it is important that teams do not
look at each other's cards or make notes to help them remember what
has been said. This emphasises the idea that everyone has a part to
play and reduces the chance of one person taking over the problem
and leaving others with nothing to do.
It is good to have an
observer in this task but, if this is not possible, the observer
check list might make a good starting point for you to use for
feedback.
The cards can be found here.
When teams have finished
working on the task it is important to spend time asking them to
discuss in groups, and then as a whole class, how well they worked
as a team, what they have learned from the experience and what they
would do differently next time. Your own observations, as well as
those of observers, might inform the discussions.
Note that it is
possible to split the two sets of information and just make one
solid at a time, as in The Solid task found here.
Key questions
- Has anyone got a card that they think has a useful piece of information to start with? Can you expain why this is a useful card?
- Have you used all the information you have been given?
- How well did you listen to others in your group?
- How easy was it to share what you knew?
Possible extension
Learners may like to try
one of the other 'All for one' tasks. Other team-building tasks can
be found by going to this article.
Possible support
Learners can reveal one
(or more) of their cards at a time. Other team-building tasks can
be found by going to this article.
You may also like
Classifying Solids Using Angle Deficiency
Toni Beardon has chosen this article introducing a rich area for practical exploration and discovery in 3D geometry
Paper Folding - Models of the Platonic Solids
A description of how to make the five Platonic solids out of paper.
The Solid
A task which depends on members of the group working collaboratively to reach a single goal.

