Skip over navigation
Torus Patterns
Age 16 to 18
Challenge Level 
This problem naturally follows on
from Painting By Numbers, although it can be attempted
independently of this.
A torus may be represented by a square with the points on the two opposite sides identified.
In this problem we consider colouring in line drawings made on the surfaces of various tori.
They are to be coloured according to the two rules:
1) No two regions of the same colour can share a border
2) Two regions of the same colour are allowed to meet at a point.
Consider the following three patterns corresponding to three tori
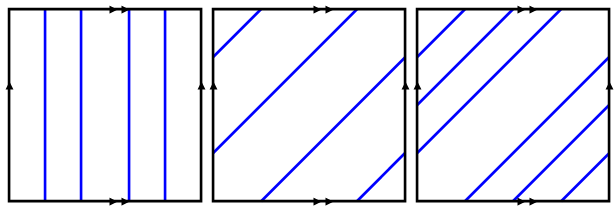
How many colours would be needed to colour the associated tori using the colouring rules above? You might wish to try to visualise the patterns on the tori, but this is not necessary.
Explore some other patterns on tori and how many colours would be needed to colour various patterns.
It is possible to create patterns which require 4, 5, 6 and 7 distinct colours to colour.
Can you create examples of such patterns?
Extension: Consider the question of painting by numbers on a Mobius strip
A torus may be represented by a square with the points on the two opposite sides identified.
In this problem we consider colouring in line drawings made on the surfaces of various tori.
They are to be coloured according to the two rules:
1) No two regions of the same colour can share a border
2) Two regions of the same colour are allowed to meet at a point.
Consider the following three patterns corresponding to three tori
How many colours would be needed to colour the associated tori using the colouring rules above? You might wish to try to visualise the patterns on the tori, but this is not necessary.
Explore some other patterns on tori and how many colours would be needed to colour various patterns.
It is possible to create patterns which require 4, 5, 6 and 7 distinct colours to colour.
Can you create examples of such patterns?
Extension: Consider the question of painting by numbers on a Mobius strip
You may also like
Where Do We Get Our Feet Wet?
Professor Korner has generously supported school mathematics for more than 30 years and has been a good friend to NRICH since it started.
Links and Knots
Some puzzles requiring no knowledge of knot theory, just a careful inspection of the patterns. A glimpse of the classification of knots, prime knots, crossing numbers and knot arithmetic.
Earth Shapes
What if the Earth's shape was a cube or a cone or a pyramid or a saddle ... See some curious worlds here.