Skip over navigation



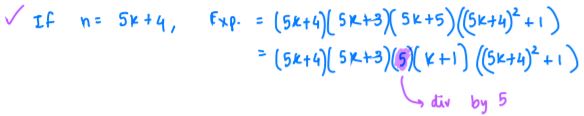





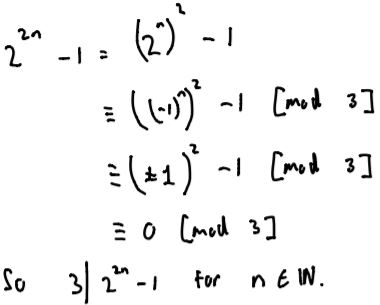

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Common Divisor
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Part A: What is the largest integer that divides $1^3 - 1$, $2^3 - 2$, $3^3 - 3$, $4^3 - 4$, $n^3 - n$?
Note that in their solutions, some people use the notation $3|12$ to mean "3 is a multiple of 12" or "3 divides 12"
Wiktor from LAE Tottenham in the UK, Mahdi from Mahatma Gandhi International School in India, Nikita from Jersey College for Girls in Jersey and David sent in similar answers. This is Wiktor's work:
Part B: What is the largest integer that divides $1^5 - 1^3$, $2^5 - 2^3$, $3^5 - 3^3$,$4^5 - 4^3$ and $n^5 - n^3$?
Nikita, David, Wiktor and Mahdi all began in the same way. This is Nikita's work:

Mahdi's proof is very similar, but David proved the statement without writing out the cases algebraically. David wrote:
$n^5-n^3 = n^3(n+1)(n-1)$
If $n$ is even, $8|n^3$
If $n$ is odd, then one of $(n-1), (n+1)$ is divisibly by $4$ and the other is divisible by $2$. So $(n-1)n^3(n+1)$ is necessarily divisible by $8.$
Part C: Find the largest integer which divides every member of the following sequence: $$ 1^5-1,\ 2^5-2,\ 3^5-3,\cdots\, n^5-n.$$
Nikita, David and Mahdi's work all begins in the same way. This is Mahdi's work:
David considered five cases without writing them out algebraically:
$n^5-n=(n-1)n(n+1)(n^2+1)$
If $n\equiv 0 \text{ (mod 5})$ then $5|n$
If $n\equiv 1 \text{ (mod 5})$ then $5|n-1$
If $n\equiv \pm 2 \text{ (mod 5})$ then $5|n^2+1$ (which means $n\equiv 2 \text{ (mod 5})$ or $n\equiv 3 \text{ (mod 5)}$
If $n\equiv 4 \text{ (mod 5})$ then $5|n+1$
Nikita used the same idea but on the unfactorised expression:

Wiktor used proof by induction:

Wiktor has shown that whenever $k^5 - k$ is a multiple of $5$, $(k+1)^5 - (k+1)$ is also a multiple of $5$. This means that for each term in the sequence that is a multiple of $5$, the following term is also a multiple of $5$. Since the first few terms are multiples of $5$, this means that all the terms in the
sequence must be multiples of $5$.
Part D: Show that $2^{2n} -1$ can always be divided by three.
Wiktor, Mahdi and Sahin sent in very similar proofs. This is Sahin's work:

Nikita and Wiktor sent in a different proof. This is Nikita's work:

(for all positive integers $n$)
David sent in a different proof, using modular arithmetic. My maths teacher would have said it's like using a sledgehammer to crack an egg:
You may also like
A Close Match
Can you massage the parameters of these curves to make them match as closely as possible?

