Skip over navigation
Akram made the longer chain because he made $6$ sets of twos ($6\times2=12$).
Daisy made only $4$ sets of twos ($4\times2=8$).
In the second example they were counting in fives.
Daisy made two sets of fives ($5\times2=10$) and Akram made $3$ sets ($5\times3=15$).
In the third example Daisy was counting in threes and Akram was counting in fours.
You can make chains counting in any number. In the picture I've shown chains with sixes, sevens, eights and nines:


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cube Bricks and Daisy Chains
Age 5 to 7
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Ria from Beijing City International School sent us a very full solution:
In the first example Daisy and Akram were counting in twos.Akram made the longer chain because he made $6$ sets of twos ($6\times2=12$).
Daisy made only $4$ sets of twos ($4\times2=8$).
In the second example they were counting in fives.
Daisy made two sets of fives ($5\times2=10$) and Akram made $3$ sets ($5\times3=15$).
In the third example Daisy was counting in threes and Akram was counting in fours.
You can make chains counting in any number. In the picture I've shown chains with sixes, sevens, eights and nines:

Thank you, Ria, although I wonder whether your pictures for counting in sixes and sevens are rather similar? Jesse and Emma from Creston thought that Akram was making a pattern of blue, yellow, red and green in the final part. Well done also to Sue-Min and Anna from the Canadian Academy who also explained their answers clearly.
You may also like
Number Round Up
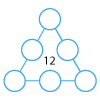
Arrange the numbers 1 to 6 in each set of circles below. The sum of each side of the triangle should equal the number in its centre.
Grouping Goodies
Pat counts her sweets in different groups and both times she has some left over. How many sweets could she have had?

