Skip over navigation
Put the first cannon at the origin $(0, 0)$ and the second cannon at the point $(D, 0)$.
Using a constant acceleration of $-g$ in the $y$-direction and $0$ in the $x$-direction it is a simple matter to write down the positions of each cannon ball at a time $t> T$ if we make use of the formula $s=ut+\frac{1}{2}at^2$.
$$
\begin{eqnarray}
(x_1, y_1)&=&\left(100\cos(45^\circ)t, 100\sin(45^\circ)t-\frac{1}{2}gt^2\right)\cr
(x_2, y_2)&=&\left(D-100\cos(30^\circ)(t-T), 100\sin(30^\circ)(t-T)-\frac{1}{2}g(t-T)^2\right)
\end{eqnarray}
$$
As with all mechanics problems, the first part involves a careful setup of the equations. Once I have checked these carefully (... OK, that's done...) we can proceed with the algebra to resolve the equations.
Since I know that the two cannon balls strike each other the plan of attack is to equate the two $x$ and $y$ coordinates. I find that
$$
50 \sqrt{2}t = D-50\sqrt{3}(t-T)
$$
and
$$
50\sqrt{2}t-5t^2=50(t-T)-5(t-T)^2\;.
$$
After some rearrangement, the second of these equations gives me
$$
\begin{eqnarray}
\left(10(\sqrt{2}-1)-2T\right)t &=& -T^2-10T\cr
\Rightarrow t = \frac{T^2+10T}{2T-10(\sqrt{2}-1)}\;.
\end{eqnarray}
$$
Since for a collision to occur we must have $t> 0$, which implies that
$$
T> 5(\sqrt{2}-1)\;.
$$
Thus, there is a minimum value of $T$ (which might be greater than $5(\sqrt{2}-1)$; it is not less than this value). Now, for a collision to occur in the air the $y$ coordinate at the point of collision must be positive. The expression for the first cannon ball quickly gives us the inequality
$$ t< 10\sqrt{2}\;.$$
This gives us a more complicated inequality for $T$ as
$$
\frac{T^2+10T}{2T-10(\sqrt{2}-1)}< 10\sqrt{2}\;.
$$
Rearranging we see that
$$T^2+10(1-2\sqrt{2})T+100(2-\sqrt{2})< 0\;.$$
Values of $T$ which satisfy this equation are those lying between the two roots
$$
T_{1, 2} = \frac{10(2\sqrt{2}-1)\pm\sqrt{(10(1-2\sqrt{2})^2-4(100(2-\sqrt{2}))}}{2}\;.
$$
Thus,
$$
10(\sqrt{2}-1) < T< 10\sqrt{2}\;.
$$
I used a spreadsheet to plot the values of $D$ against $T$. The range of permissible values is
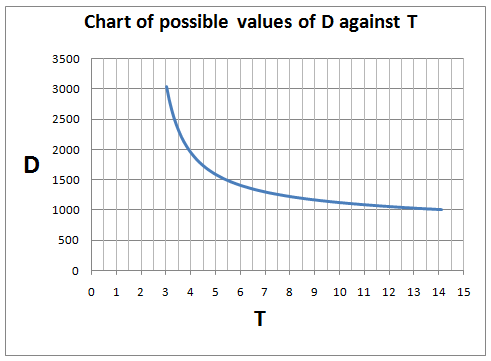

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Crazy Cannons
Age 16 to 18
ShortChallenge Level 





- Problem
- Solutions
Put the first cannon at the origin $(0, 0)$ and the second cannon at the point $(D, 0)$.
Using a constant acceleration of $-g$ in the $y$-direction and $0$ in the $x$-direction it is a simple matter to write down the positions of each cannon ball at a time $t> T$ if we make use of the formula $s=ut+\frac{1}{2}at^2$.
$$
\begin{eqnarray}
(x_1, y_1)&=&\left(100\cos(45^\circ)t, 100\sin(45^\circ)t-\frac{1}{2}gt^2\right)\cr
(x_2, y_2)&=&\left(D-100\cos(30^\circ)(t-T), 100\sin(30^\circ)(t-T)-\frac{1}{2}g(t-T)^2\right)
\end{eqnarray}
$$
As with all mechanics problems, the first part involves a careful setup of the equations. Once I have checked these carefully (... OK, that's done...) we can proceed with the algebra to resolve the equations.
Since I know that the two cannon balls strike each other the plan of attack is to equate the two $x$ and $y$ coordinates. I find that
$$
50 \sqrt{2}t = D-50\sqrt{3}(t-T)
$$
and
$$
50\sqrt{2}t-5t^2=50(t-T)-5(t-T)^2\;.
$$
After some rearrangement, the second of these equations gives me
$$
\begin{eqnarray}
\left(10(\sqrt{2}-1)-2T\right)t &=& -T^2-10T\cr
\Rightarrow t = \frac{T^2+10T}{2T-10(\sqrt{2}-1)}\;.
\end{eqnarray}
$$
Since for a collision to occur we must have $t> 0$, which implies that
$$
T> 5(\sqrt{2}-1)\;.
$$
Thus, there is a minimum value of $T$ (which might be greater than $5(\sqrt{2}-1)$; it is not less than this value). Now, for a collision to occur in the air the $y$ coordinate at the point of collision must be positive. The expression for the first cannon ball quickly gives us the inequality
$$ t< 10\sqrt{2}\;.$$
This gives us a more complicated inequality for $T$ as
$$
\frac{T^2+10T}{2T-10(\sqrt{2}-1)}< 10\sqrt{2}\;.
$$
Rearranging we see that
$$T^2+10(1-2\sqrt{2})T+100(2-\sqrt{2})< 0\;.$$
Values of $T$ which satisfy this equation are those lying between the two roots
$$
T_{1, 2} = \frac{10(2\sqrt{2}-1)\pm\sqrt{(10(1-2\sqrt{2})^2-4(100(2-\sqrt{2}))}}{2}\;.
$$
Thus,
$$
10(\sqrt{2}-1) < T< 10\sqrt{2}\;.
$$
I used a spreadsheet to plot the values of $D$ against $T$. The range of permissible values is
You may also like
A Close Match
Can you massage the parameters of these curves to make them match as closely as possible?

