Skip over navigation
Differentiating gives
$$f'(x) = \sin(\sin(\cos x)) \cdot \cos(\cos(x)) \cdot \sin(x)$$
This is zero if and only if
$$\sin(\sin(\cos x))=0 \mbox{ or } \cos(\cos(x)) = 0 \mbox{ or } \sin(x)=0$$
Consider the first of these three conditions:
$$\sin(\sin(\cos x))=0 \Rightarrow \sin(\cos x) = n\pi, n\in \mathbb{Z}$$
Since $|\sin(X)|\leq 1$ for any real $X$ and $\pi > 1$ we must choose $n=0$ in the previous equation.
Thus,
$$\sin(\sin(\cos x))=0 \Rightarrow \sin(\cos x) = 0 \Rightarrow \cos x = m\pi, m\in \mathbb{Z}$$
Similarly, we must choose $m=0$ in this expression. We can thus conclude that
$$\sin(\sin(\cos x))=0 \Leftrightarrow x = \left(r+\frac{1}{2}\right)\pi, r \in \mathbb{Z}$$
Consider the second of the three conditions:
$$\cos(\cos(x)) = 0 \Leftrightarrow \cos(x) = \left(r+\frac{1}{2}\right)\pi, r \in \mathbb{Z}$$
Since $\frac{1}{2}\pi> 1$ there are no real solutions to this condition.
Consider the third of the three conditions:
$$\sin(x) =0 \Leftrightarrow x = n\pi, n \in \mathbb{Z}$$
Combining all three conditions gives us the locations of the turning points:
$$
f'(x)=0 \Leftrightarrow x = \frac{N\pi}{2}, N\in \mathbb{Z}
$$
We now need to consider whether they are maxima, minima or something else. We could look at the second derivative, but this will be complicated and the boundedness of $\sin(x)$ and $\cos(x)$ allows us to make shortcuts as follows:
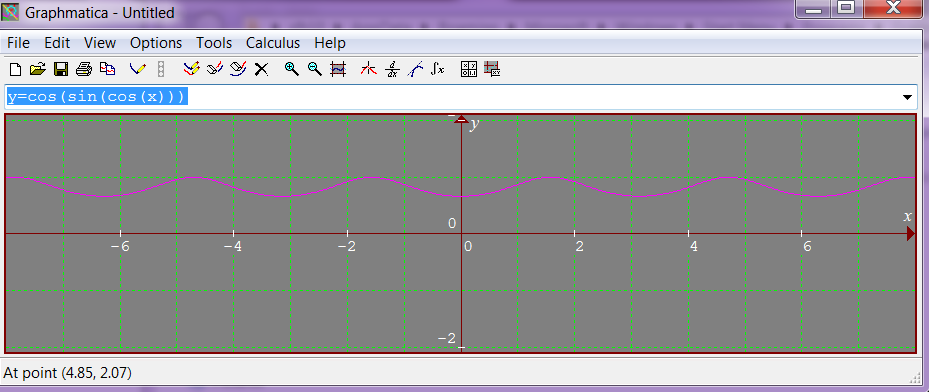
Notice that $f(x) = 1$ when $x = \pm \frac{\pi}{2}, \pm \frac{3\pi}{2}, \pm \frac{5\pi}{2}, \dots$. Since $f(x)$ is continuous and differentiable and $|f(x)|\leq 1$ these points must be maxima. The even multiples of $\frac{\pi}{2}$ must therefore be minima, at which the function takes the values $f(x) = \cos(\sin 1) \approx 0.666$.
A plot of the graph confirms this calculation:

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Trig Trig Trig
Age 16 to 18
ShortChallenge Level 





- Problem
- Solutions
Differentiating gives
$$f'(x) = \sin(\sin(\cos x)) \cdot \cos(\cos(x)) \cdot \sin(x)$$
This is zero if and only if
$$\sin(\sin(\cos x))=0 \mbox{ or } \cos(\cos(x)) = 0 \mbox{ or } \sin(x)=0$$
Consider the first of these three conditions:
$$\sin(\sin(\cos x))=0 \Rightarrow \sin(\cos x) = n\pi, n\in \mathbb{Z}$$
Since $|\sin(X)|\leq 1$ for any real $X$ and $\pi > 1$ we must choose $n=0$ in the previous equation.
Thus,
$$\sin(\sin(\cos x))=0 \Rightarrow \sin(\cos x) = 0 \Rightarrow \cos x = m\pi, m\in \mathbb{Z}$$
Similarly, we must choose $m=0$ in this expression. We can thus conclude that
$$\sin(\sin(\cos x))=0 \Leftrightarrow x = \left(r+\frac{1}{2}\right)\pi, r \in \mathbb{Z}$$
Consider the second of the three conditions:
$$\cos(\cos(x)) = 0 \Leftrightarrow \cos(x) = \left(r+\frac{1}{2}\right)\pi, r \in \mathbb{Z}$$
Since $\frac{1}{2}\pi> 1$ there are no real solutions to this condition.
Consider the third of the three conditions:
$$\sin(x) =0 \Leftrightarrow x = n\pi, n \in \mathbb{Z}$$
Combining all three conditions gives us the locations of the turning points:
$$
f'(x)=0 \Leftrightarrow x = \frac{N\pi}{2}, N\in \mathbb{Z}
$$
We now need to consider whether they are maxima, minima or something else. We could look at the second derivative, but this will be complicated and the boundedness of $\sin(x)$ and $\cos(x)$ allows us to make shortcuts as follows:
Notice that $f(x) = 1$ when $x = \pm \frac{\pi}{2}, \pm \frac{3\pi}{2}, \pm \frac{5\pi}{2}, \dots$. Since $f(x)$ is continuous and differentiable and $|f(x)|\leq 1$ these points must be maxima. The even multiples of $\frac{\pi}{2}$ must therefore be minima, at which the function takes the values $f(x) = \cos(\sin 1) \approx 0.666$.
A plot of the graph confirms this calculation:

You may also like
A Close Match
Can you massage the parameters of these curves to make them match as closely as possible?

