Skip over navigation
We are looking to sketch $y=\cos(\tan(x))$.
What do we know about this? Certainly we will have $-1\leq y\leq 1$ since $\cos(x)$ is always between $-1$ and $1$, regardless of its arguament.
Next, we know that $\cos(\theta)$ is zero for the values $\theta = (2n+1)\frac{\pi}{2}$ and has turning points inbetween these values at $m\pi$
Next, we know that $\tan{x}$ has asymptotes at $x = \pm \frac{\pi}{2}, \pm\frac{3\pi}{2}$. Only two of these lie in the range $-\pi \leq x \leq \pi$. This allows us to see that $\tan x$ takes every real number value exactly twice on the range $-\pi < x \leq \pi$ and is undefined at two points on this range.
Thus, $y=\cos(\tan x)$ will have an infinite number of turning points on the specified range, and these occur precisely at the values
$$
0, \pm\tan^{-1}(\pi), \pm \tan^{-1} (2\pi), \pm \tan^{-1}(3\pi) \dots
$$
Numerically, these values are
$$
0, \pm 1.262627, \pm 1.412965, \pm 1.465089, \pm 1.491386, \pm 1.50720, \pm 1.517794, \dots
$$
Note that these values tend to the numbers $\pm \frac{\pi}{2}$, which are the two values for which our function is undefined
Similarly, zeros will occur at the values
$$
\pm\tan^{-1}\left(\frac{\pi}{2}\right),\tan^{-1}\left(\frac{3\pi}{2}\right), \tan^{-1}\left(\frac{5\pi}{2}\right)\dots
$$
Putting all this together we obtain a bounded function which oscillates infinitely often in any interval containing the point $\frac{\pi}{2}$ or the point -$\frac{\pi}{2}$
The final part is to determine which points are maxima and which are minima. This is easily done by evaluating $\cos(\tan(0)) = +1$ and $\cos(\tan(\pm\pi))=1$.
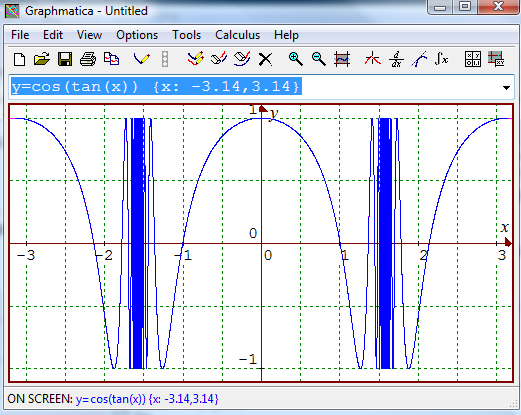
The key points can easily be indicated with paper and pencil, but here is the output from graphmatica so that you can check your answers.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Trigger
Age 16 to 18
ShortChallenge Level 





- Problem
- Getting Started
- Solutions
We are looking to sketch $y=\cos(\tan(x))$.
What do we know about this? Certainly we will have $-1\leq y\leq 1$ since $\cos(x)$ is always between $-1$ and $1$, regardless of its arguament.
Next, we know that $\cos(\theta)$ is zero for the values $\theta = (2n+1)\frac{\pi}{2}$ and has turning points inbetween these values at $m\pi$
Next, we know that $\tan{x}$ has asymptotes at $x = \pm \frac{\pi}{2}, \pm\frac{3\pi}{2}$. Only two of these lie in the range $-\pi \leq x \leq \pi$. This allows us to see that $\tan x$ takes every real number value exactly twice on the range $-\pi < x \leq \pi$ and is undefined at two points on this range.
Thus, $y=\cos(\tan x)$ will have an infinite number of turning points on the specified range, and these occur precisely at the values
$$
0, \pm\tan^{-1}(\pi), \pm \tan^{-1} (2\pi), \pm \tan^{-1}(3\pi) \dots
$$
Numerically, these values are
$$
0, \pm 1.262627, \pm 1.412965, \pm 1.465089, \pm 1.491386, \pm 1.50720, \pm 1.517794, \dots
$$
Note that these values tend to the numbers $\pm \frac{\pi}{2}$, which are the two values for which our function is undefined
Similarly, zeros will occur at the values
$$
\pm\tan^{-1}\left(\frac{\pi}{2}\right),\tan^{-1}\left(\frac{3\pi}{2}\right), \tan^{-1}\left(\frac{5\pi}{2}\right)\dots
$$
Putting all this together we obtain a bounded function which oscillates infinitely often in any interval containing the point $\frac{\pi}{2}$ or the point -$\frac{\pi}{2}$
The final part is to determine which points are maxima and which are minima. This is easily done by evaluating $\cos(\tan(0)) = +1$ and $\cos(\tan(\pm\pi))=1$.
The key points can easily be indicated with paper and pencil, but here is the output from graphmatica so that you can check your answers.

You may also like
A Close Match
Can you massage the parameters of these curves to make them match as closely as possible?

