Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Peas in a Pod



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Just using the table, we know that parent 1 had two Y genes and grandparent 4 had two s genes, because yellow and short genes are both recessive. So parent 2 must have inherited a short gene from grandparent 4, which means that parent 2's height genes must be ts. The tall gene must have come from grandparent 3, so grandparent 3 must have been tall.
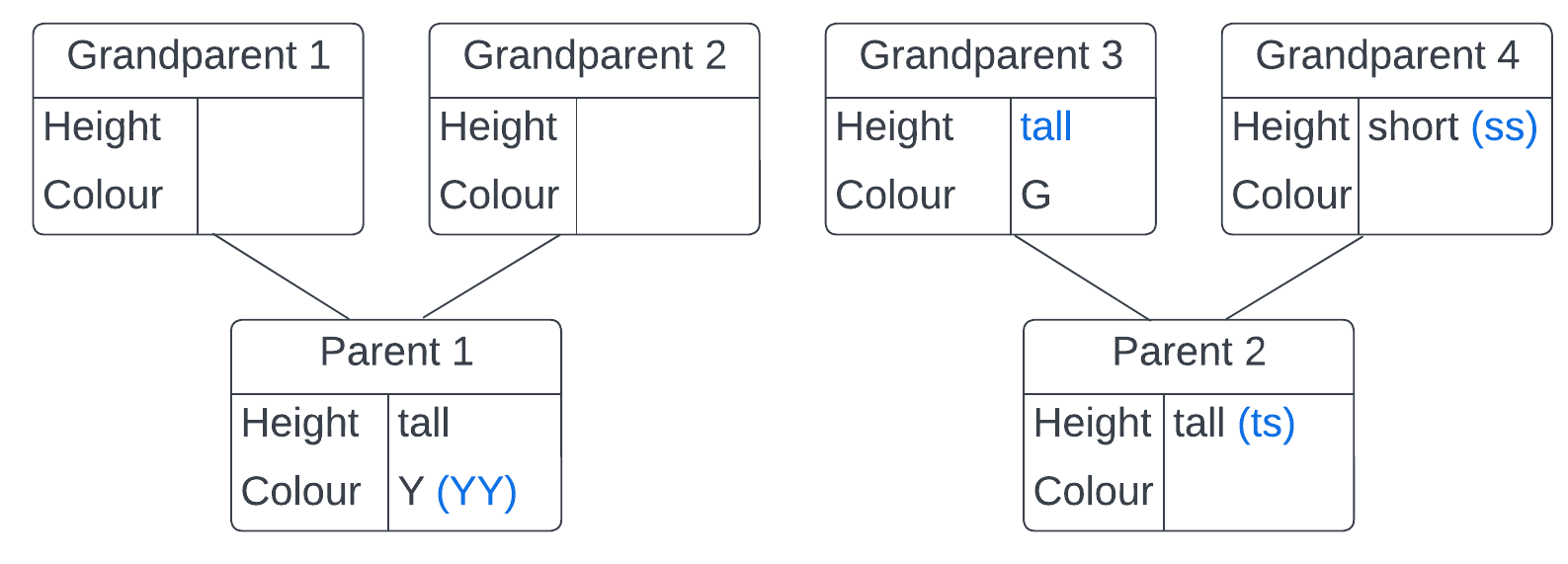
She knows it won't be the same height and the same colour as grandparent 3.
This means the plant can't be tall and green. We know it could be tall, because both its parents were tall. Therefore it can't be green. Green is dominant, so parent 2 must have been yellow.
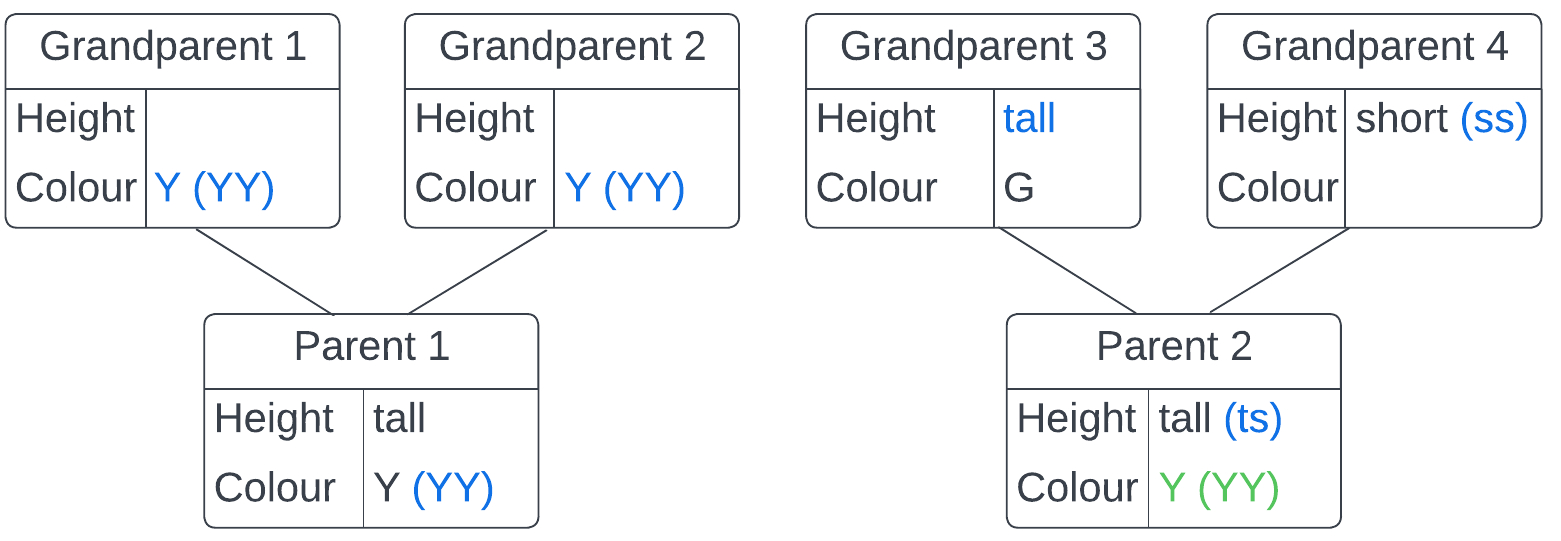
Coola knows that there is a small chance the plant will be the same height and colour as grandparent 1, but it is more likely it will be the same height and colour as parent 1.
The plant will certainly be yellow, and it is more likely to be tall than short. Therefore grandparent 1 must have been short.
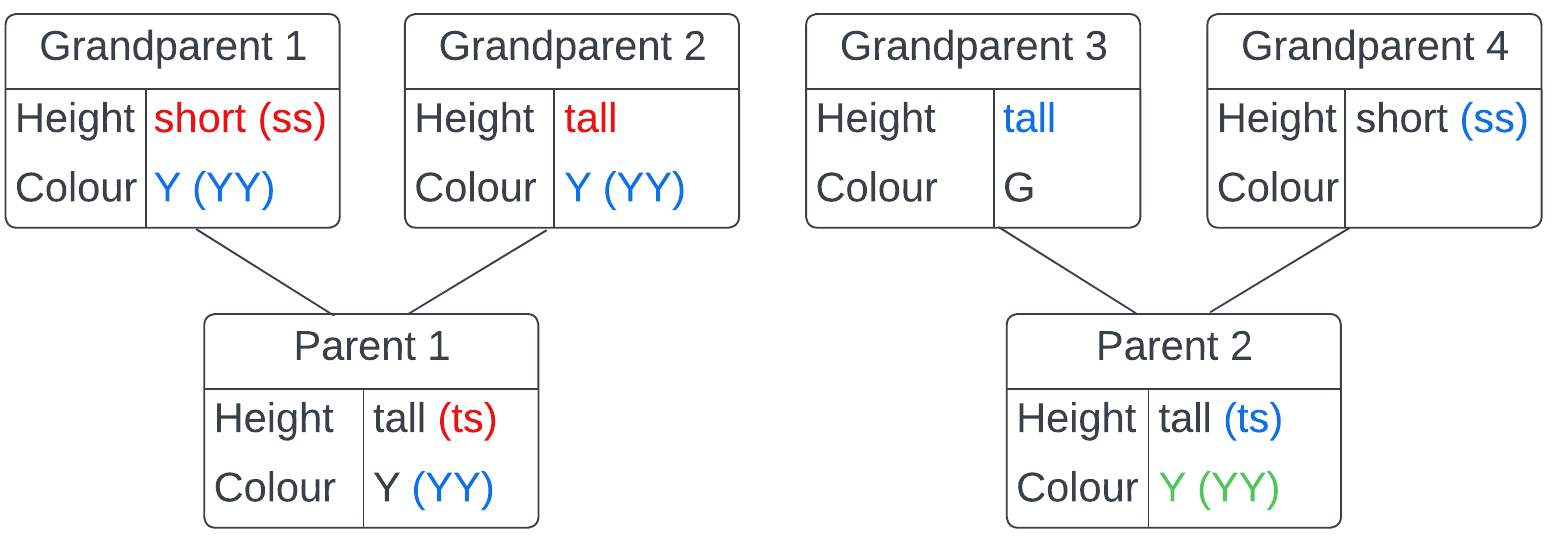
1. Can you determine the colour of parent 2? Yellow
2. Can you describe the height of grandparents 1 and 2? Grandparent 1 was short and grandparent 2 was tall
3. How likely is it that the pea will grow into a short yellow plant? For this to happen, the pea must have a short gene from parent 1 (1 in 2 chance) and a short gene from parent 2 (1 in 2 chance). Therefore the probability of it growing into a short plant is 1 in 4. It will definitely be yellow, so the answer is 1 in 4. This is also shown in the table below.
| parent 1 short gene |
parent 1 tall gene |
|
|---|---|---|
| parent 2 short gene |
short (ss) | tall (ts) |
| parent 2 tall gene |
tall (ts) | tall (tt) |
4. How likely is it that the plant will be green? Impossible
You may also like
Gambling at Monte Carlo
A man went to Monte Carlo to try and make his fortune. Is his strategy a winning one?
Marbles and Bags
Two bags contain different numbers of red and blue marbles. A marble is removed from one of the bags. The marble is blue. What is the probability that it was removed from bag A?
Coin Tossing Games
You and I play a game involving successive throws of a fair coin. Suppose I pick HH and you pick TH. The coin is thrown repeatedly until we see either two heads in a row (I win) or a tail followed by a head (you win). What is the probability that you win?

