The Why and How of Substitution

Introduction 
  
"How could I have seen that?" This is a common response to seeing a substitution in mathematics, and this article attempts to answer this question. Sadly, the technique of substitution is often presented without mentioning the general idea behind all substitutions. The effective use of substitution depends on two things: first, given a situation in which variables occur, a substitution is nothing more than a change of variable; second, it is only effective if the change of variable simplifies the situation and, hopefully, enables one to solve the simplified problem.

There is no easy route to this: substitution will only work if the the original situation has some kind of symmetry or special property that we can exploit, and the skill in using the method of substitution depends on noticing this. Thus we should always be looking for special features in the problem, and then be prepared to change the variable(s) to exploit these features. Of course, once we have solved the problem in the new variables we have to rewrite the solution in terms of the original variables.

The main idea behind substitution, then, is this. We are given some expression, or equation or graph involving the variable $x$. We make the substitution $x = f(t)$, and we now have a new expression, equation or graph involving the given terms, the variable $t$ and the function $f$. Since we are free to choose $f$ to be any function we like, it is highly likely that for a suitable choice of $f$ the new expression in $t$ will be simpler than the original expression in $x$. The skill lies in the selection of $f$; the rest is just the algebraic manipulation of the variables.

Let us now look at some examples with these ideas in mind.
 
Example $1$ Polynomial Equations 
  
Let us consider the polynomial equation

$$(x-1)(x-4)(x-6)(x-9)= a.$$
If we expand the left hand side we get a quartic in $x$ which we cannot solve. However, we notice that the left hand side has a certain symmetry, namely $1+9=4+6$. The roots of the left hand side are symmetric about the value $5$, and this suggests that we should make a substitution that exploits this fact. Let us try $x=s+5$; that is, we change the variable so that the symmetry is now about the origin (after all, $5-1$ and $5+1$ looks better than $4$ and $6$). With this we have
$$(s+4)(s+1)(s-1)(s-4) = a,$$
or $(s^2-1)(s^2-16) = a$. This is a quadratic equation in $s^2$ which we can solve to give two values of $s^2$ and four values of $s$ corresponding to the four solutions to the original equation. However, we can also simplify it with another substitution. The numbers $1$ and $16$ are symmetric about $17/2$ so we now make the substitution $s^2=t + \frac{17}{2}$. This gives $t^2 = a+\frac{225}{4}$ so that $$\begin{eqnarray*} t &=& \pm \sqrt{a +\frac{225}{4}},\\ s &=& \pm\sqrt{\frac{17}{2}\pm \sqrt{a +\frac{225}{4}}},\\ x &=& 5 \pm\sqrt{\frac{17}{2}\pm \sqrt{a +\frac{225}{4}}}. \end{eqnarray*}$$
You should check that if we put $a=0$ in this formula we do get  the expected solutions $1,4,6,9$. What do you get if $a=216$?
 
Example $2$ Rational functions 
 
We want to solve the following equation:
$\frac{x^2-10x+15}{x^2-6x+15} = \frac{3x}{x^2-8x+15}.$
By clearing fractions this becomes a quartic equation which is difficult to solve. Observing the occurrences of $x^2+15$, and the symmetry of $x^2-6x+15$, $x^2-8x+15$ and $x^2-10x+15$, we can turn this into a quadratic equation by substituting $t= x-8 + \frac{15}{x}$. We get the equation
$$\frac{t-2}{t+2}=\frac{3}{t}.$$
This simplifies to $t^2-5t-6=0$, so that $t$ is $6$ or $-1$. Each value of $t$ gives a quadratic equation in $x$, giving four solutions of the original equation in $x$. The two quadratic equations are $$x-8+\frac{15}{x}=6, \qquad x-8+\frac{15}{x}=-1.$$
These equations simplify to
$$x^2-14x+15-0, \qquad x^2-7x+15=0,$$
and the four solutions are $$7 \pm\sqrt{34}, \quad \frac{1}{2}\big(7\pm i\sqrt{11}\big).$$  

Example $3$ Integration by substitution  
 
Evaluate $I = \int (1-9x^2)^{1/2}\,dx.$
Here a trigonometric substitution leads to a simpler integral. Because of the relation $1-\sin^2 u = \cos^2 u$, we substitute $3x = \sin u$ and $3dx = \cos u\,du$ and get
$$\begin{eqnarray*} I &=& \int \big(1-\sin^2u\big)^{1/2}\times \big(\frac{1}{3}\cos u\big)\, du\\ &=& \int \frac{1}{3}\cos^2 u\,du \\ &=& \frac{1}{3}\int\frac{1}{2}(1+\cos 2u)\,du\\ &=& \frac{1}{6}(u + \frac{1}{2}\sin 2u)+k.. \end{eqnarray*}$$
To return to an expression in terms of $x$ we use $\sin 2u = 2\sin u\,\cos u = 6x(1-9x^2)^{1/2}$, and the integral we want is
$$I = \frac{1}{6}\sin^{-1}3x + \frac{1}{2}x\big(1-9x^2\big)^{1/2} + k.$$

Example $4$ Area inside an ellipse

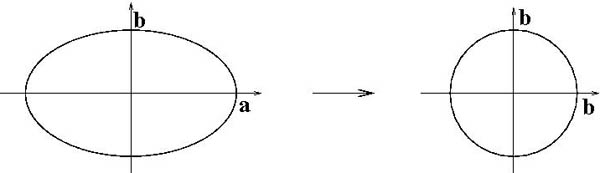
In order to find the the area inside the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, we can use the transformation $(x,y) \to (\frac{ax}{b},y)$ to change the ellipse into a circle. Since the lengths in the $x$-direction are changed by a factor $\frac{b}{a}$, and the lengths in the $y$-direction remain the same, the area is changed by a factor $\frac{b}{a}$. Thus
$$\text{Area of circle} = \frac{b}{a}\times \text{Area of ellipse},$$
which gives the area of the ellipse as $(\frac{a}{b} \times \pi b^2)$, that is  $\pi ab$.
 
Example $5$  Polynomial   
 
Consider a general polynomial $$p(x) = a_0 + a_1x + a_2x^2 +\cdots +a_{n-1}x^{n-1} + a_nx^n.$$ Let us make the substitution $x=t+k$, where $k$ is a constant which we shall determine later. Now write $p(x) = p(t+k)=q(t)$. Then
$$\begin{eqnarray*} q(t) &=& a_n(t+k)^n + a_{n-1}(t+k)^{n-1} + \cdots +a_1(t+k)+a_0\\ &=& \big(a_nt^n + na_nkt^{n-1} + \cdots) + a_{n-1}t^{n-1} + \cdots\\ &=& a_nt^n + \big(na_nk+ a_{n-1}\big)t^{n-1} +\cdots, \end{eqnarray*}$$
where here "$\cdots$'' means powers of $t$ of order $n-2$ or less. If we now choose $k= -a_{n-1}/na_n$ we see that
$$q(t) = a_nt^n + b_{n-2}t^{n-2} + \cdots + b_1t + b_0;$$
in other words, by changing the variable we can remove the term of degree $n-1$. While the effect of this substitution may not seem spectacular, it is important. It is exactly what we do when we 'complete the square'  to solve quadratic equations, and this is the method used to find the formula for the roots of a quadratic equation. It is also the first step in solving cubic equations, for there it says that we only need consider equations of the form $x^3 + bx +c=0$.

Finally, it is worth noting that the coefficient of $x^{n-1}$ in a polynomial equation of degree $n$ is minus the sum of the roots of the equation so this substitution is such that the chosen value of $k$ is the average value of the roots of the polynomial.

Example $6$ Transformations of the plane  
In Example $5$ we showed how to remove the term in $x^{n-1}$ from a polynomial of degree $n$. Now we are going to show how, given the equation of a conic, for example,
$$x^2 +2bxy + y^2=1, \quad (1)$$
we can remove the $xy$ term and so more easily discover the properties of the conic. First, if we make the substitution 
$$x = \frac{1}{\sqrt{2}}(u-v), \quad y = \frac{1}{\sqrt{2}}(u+v), \quad (2)$$ we see that $(1)$ becomes
$$u^2(1+b) + v^2(1-b)=1. \quad (3)$$
Thus equation $(1)$ gives an ellipse if $|b|< 1$, a hyperbola if $|b|> 1$, and it reduces to a pair of lines if $|b|=1$. The question, however, is (as at the start of this article) "How could I have seen this?" We are going to change the variables $x,y$ to new variables $u,v$ by rotating the plane by an angle $\theta$. As we do not yet know which value $\theta$ to take, we work with a general $\theta$ and make this choice later. A rotation of the plane by an angle $\theta$ is given by
$$x = u\cos\theta - v\sin\theta,\quad y = u\sin\theta + v\cos\theta. \quad (4)$$
If we substitute these in equation $(1)$ we obtain
$$(1+b\sin 2\theta)u^2 +(2b\cos 2\theta)uv +(1-b\sin 2\theta)v^2 =1,$$
and so if we now choose $\theta$ so that $\cos 2\theta =0$, we see that the $uv$ term will vanish. Thus we take $\theta = \pi/4$, and this with $(4)$ gives the values of $x$ and $y$ as in $(2)$ and hence the equation of the conic as in $(3)$.

More generally, if we have an equation
$$ax^2 +bxy +cy^2 +dx +ey +f =0, \quad (5)$$ where $a,b,c,d,e,f$ are real numbers, we can try to remove the linear terms by a translation, say $x=x_0+t$ and $y=y_0+s$, and then apply the method given above. In this way, by a combination of a translation and a rotation, we can change the variables so that the conic $(5)$ is given in a simpler form centred at the origin with the $x$ and $y$ axes as the axes of symmetry of the conic.