Curve Hunter
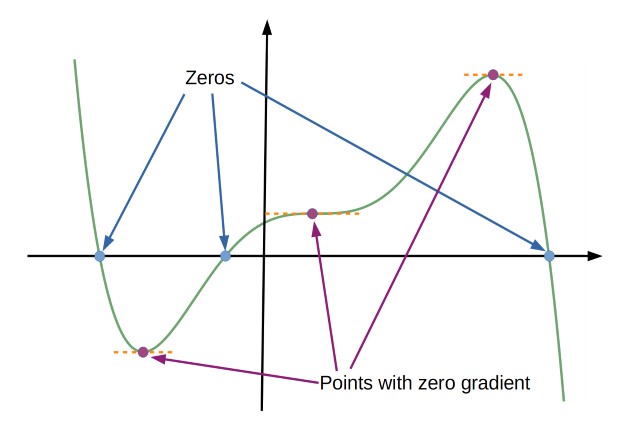
A Continuous Curve is one where the curve has no "breaks" in it, in other words you could draw the entire curve without taking your pencil off the paper. An example of a curve which is not continuous is $y=\frac 1 x$. The picture below shows a continuous curve with 3 zeros (where the curve crosses the x axis), and 3 points with zero gradient (where the curve is momentarily horizontal).
Sketch possible curves that satisfy the following conditions:
- A continuous curve with exactly one point with zero gradient and exactly two zeros.
- A continuous curve with no points with zero gradient and exactly one zero.
- A continuous curve with exactly one point with zero gradient and no zeros.
- A continuous curve with exactly two points with zero gradient and exactly three zeros.
- A continuous curve with exactly two points with zero gradient and exactly two zeros.
- A continuous curve with exactly one point with zero gradient and exactly one zero.
- A continuous curve with exactly two points with zero gradient and exactly one zero.
- A continuous curve with exactly two points with zero gradient and no zeros.
Is there a number of zeros and a number of points with zero gradient for which a continuous curve cannot be drawn? Or is it possible to draw a continuous curve with any number of zeros and any number of points with zero gradient?
Extension
Can you give examples of algebraic equations that satisfy each of the conditions above? You might like to use Desmos to try out some possible equations.
You may also like
2D-3D
Two circles of equal size intersect and the centre of each circle is on the circumference of the other. What is the area of the intersection? Now imagine that the diagram represents two spheres of equal volume with the centre of each sphere on the surface of the other. What is the volume of intersection?
Power Up
Show without recourse to any calculating aid that 7^{1/2} + 7^{1/3} + 7^{1/4} < 7 and 4^{1/2} + 4^{1/3} + 4^{1/4} > 4 . Sketch the graph of f(x) = x^{1/2} + x^{1/3} + x^{1/4} -x
Fractional Calculus I
You can differentiate and integrate n times but what if n is not a whole number? This generalisation of calculus was introduced and discussed on askNRICH by some school students.