Skip over navigation
A particle moves in a straight line under the action of a unknown force and its motion is observed in various situations.
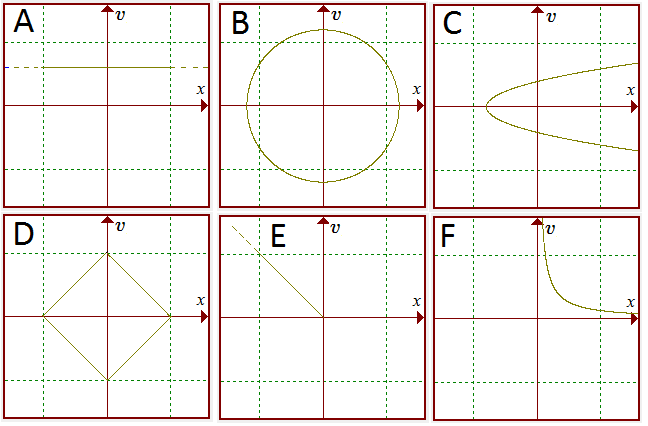
The position $x$ of the particle is plotted against its velocity $v$ for the motion in the following 6 cases.
In each case, what can you say about the motion of the particle?
In which way does each travel along the curve?
Can you think of a plausible physical interpretation for each?
What can you deduce about points corresponding to equal time intervals of the motion?
Next consider the velocity-position diagrams for the following situations:
1. A rubber ball dropped perpendicular to a hard concrete floor (if you know about coefficients of restitution, you could draw this motion accurately for $e=0.7$, neglecting all friction and air resistance).
2. A large parcel dropped from a stationary and very high helicopter.
3. An air hockey puck struck hard and perpendicular to a side on an air hockey table.
Extension: Think more generally about the meaning of velocity-position diagrams and the relationship to speed-time diagrams.

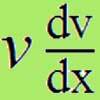
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Phase Space
Age 16 to 18
Challenge Level 





- Problem
- Student Solutions
A particle moves in a straight line under the action of a unknown force and its motion is observed in various situations.
The position $x$ of the particle is plotted against its velocity $v$ for the motion in the following 6 cases.
In each case, what can you say about the motion of the particle?
In which way does each travel along the curve?
Can you think of a plausible physical interpretation for each?
What can you deduce about points corresponding to equal time intervals of the motion?

Next consider the velocity-position diagrams for the following situations:
1. A rubber ball dropped perpendicular to a hard concrete floor (if you know about coefficients of restitution, you could draw this motion accurately for $e=0.7$, neglecting all friction and air resistance).
2. A large parcel dropped from a stationary and very high helicopter.
3. An air hockey puck struck hard and perpendicular to a side on an air hockey table.
Extension: Think more generally about the meaning of velocity-position diagrams and the relationship to speed-time diagrams.
You may also like
High Jumping
How high can a high jumper jump? How can a high jumper jump higher without jumping higher? Read on...
Out in Space
A space craft is ten thousand kilometres from the centre of the Earth moving away at 10 km per second. At what distance will it have half that speed?

