Skip over navigation

How Odd

Age 5 to 7

Challenge Level Yellow star

Primary curriculum

How Odd

How Odd printable sheet

How many odd numbers are there between 3 and 11?

How many odd numbers are there between 4 and 11?

What do you notice? Can you explain your observation?

Can you find any other pairs of numbers which have this same number of odds between them?

Can you find a pair of numbers which have four odd numbers between them?

Can you find another pair of numbers which have four odds between them? And another pair?

How would you find a pair of numbers that have five odds between them? Six odds?

How would you explain to someone else how to find a pair of numbers that have a certain number of odds between them?

Why do this problem?

This problem will help consolidate children's understanding of, and familiarity with, odd and even numbers. It also provides an opportunity for learners to explain and generalise.

Possible approach

Depending on your pupils' past experience, you may want to begin with some models of some numbers made from multilink cubes. You could put the cubes together so that they are paired, for example this would be the model for 9:

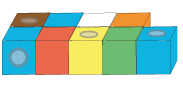
Nine blocks arranged as a row of four and a row of five

Put your multilink models out for the children to see and invite them to talk about the models. You could lead on to ordering the models numerically and pupils could make their own models to fill in some of the missing numbers.

Having made, for example, models of the numbers from 1 to 12 and placed them in numerical order, you could pose a few questions to focus on odds and evens, if this has not already come up in conversation. For instance, you could ask whether there is anything the same about any of the models. Alternatively, you could group the models into two sets, one of odds and one of evens and invite the group to talk about what you've done.

You could then pose the first challenge in the problem and step back for learners to have a go in pairs. You may need to have a conversation about what 'between' means, so that, for example, the whole numbers between 3 and 11 would not include 3 or 11. Allow them to choose how they tackle it - this will be a great assessment opportunity for you. Once they have had sufficient time, talk together about their methods and conclusions. You can then go on to the other parts of the problem, again leaving it up to the children to decide how they approach it and how they record their solutions. If possible, give the group plenty of time to find lots of examples at each stage.

You could leave the final part of the problem to the plenary. Talk together about ways of finding two numbers which have, for example, ten odds between them. You may be able to encourage some children to articulate how they would find a pair with any number of odds between them.

Key questions

How will you find out how many odd numbers there are between 3 and 11, 4 and 11 etc.?

Tell me about what you're doing.

How will you remember what you've found so far?

Possible extension

You could challenge some children to find good ways of predicting the number of odd numbers between any two numbers. How about investigating the number of even numbers between a pair of numbers?

Possible support

It would be good to have multilink and number lines available along with plenty of blank paper and pencils and small whiteboards. Of course some children may want to use particular equipment which you hadn't thought of, so do allow them to choose whatever suits them best.

Related Collections

Back to NRICH at Every Stage resources

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

How Odd

How Odd

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

Related Collections

You may also like

I'm Eight

Let's Investigate Triangles

Noah