Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Button-up



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
You found several different ways to help find the solution to this problem.
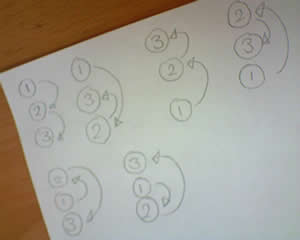
Lydia and Megan from Moorfield drew pictures of the buttons and numbered each button according to the order it was done up. They found six ways:
Some of you described the buttons as 'top', 'middle' and 'bottom' then made a list of all the possible ways of doing them up. For example, Abbie from Oakthorpe Primary said:
top bottom middle
If we start with the middle button:
middle bottom top
middle top bottom
If we start with the bottom button:
bottom top middle
bottom middle top
Then there were those of you who labelled your buttons as $1$, $2$ and $3$, like Yousef at Levendale Primary who wrote:
Karnan from Stag Lane Junior School explained how he knew he had all the possibilities:
These are all the combinations for the buttons. You can be sure because all you have to do is:1. See how many combinations there are for buttoning the top button on first.
2. Then, you have to multiply by three for three possible starting positions.
Well done all of you. Kurtis from Moorfield School and Demi from Tudhoe Grange rightly pointed out that we were presuming we wanted to do up all three buttons. Kurtis asks:
Perhaps you could find out how many ways there are if you were allowed to do up $1$, $2$ or $3$ buttons?What a great question, Kurtis!
You may also like
Plants
Three children are going to buy some plants for their birthdays. They will plant them within circular paths. How could they do this?
Triangle Animals
How many different ways can you find to join three equilateral triangles together? Can you convince us that you have found them all?
Junior Frogs
Have a go at this well-known challenge. Can you swap the frogs and toads in as few slides and jumps as possible?

