Skip over navigation
ZaynabӬ from Parkhill Junior School wrote:Ӭ
First of all I calculated how many squares there were of each colour.
Working out how many squares there were in the top part was the hardest as I had to make sure that I didn't overlap the squares.
In total there were:
Outer sides: 128 squares
Bottom: 64 squares
Top: 192 squares.
Within the top section, the colours were as follows:
Orange: 40
Green: 40
Purple: 64
I reduced the scale factor, and divided everything by 4. That way I could make a reasonably sized model. I drew it onto squared paper, then recreated it to make sure everything fit. I did this so that I could visualise it, as if I were really wrapping the auditorium.
Matthew from Dulwich College Suzhou in China sent in this picture:
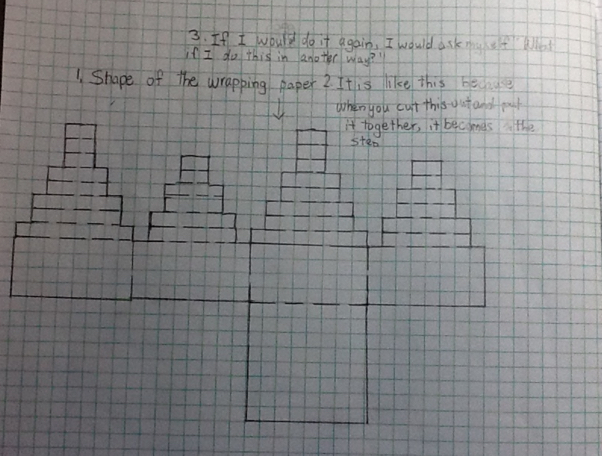
Saksham from Hounslow Town Primary School sent in this picture:
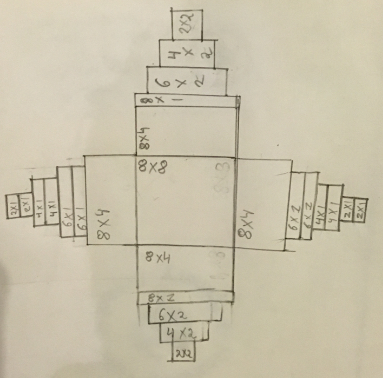
Thank you for these good solutions that probably tested your visualising skills.
Auditorium Steps
Age 7 to 14
Challenge Level 
ZaynabӬ from Parkhill Junior School wrote:Ӭ
First of all I calculated how many squares there were of each colour.
Working out how many squares there were in the top part was the hardest as I had to make sure that I didn't overlap the squares.
In total there were:
Outer sides: 128 squares
Bottom: 64 squares
Top: 192 squares.
Within the top section, the colours were as follows:
Orange: 40
Green: 40
Purple: 64
I reduced the scale factor, and divided everything by 4. That way I could make a reasonably sized model. I drew it onto squared paper, then recreated it to make sure everything fit. I did this so that I could visualise it, as if I were really wrapping the auditorium.
Matthew from Dulwich College Suzhou in China sent in this picture:
Saksham from Hounslow Town Primary School sent in this picture:
Thank you for these good solutions that probably tested your visualising skills.
You may also like
Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?