Skip over navigation
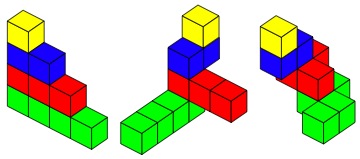
Looking at the three models here you may see that they have a lot in common although they are obviously different.
Four Layers
Age 5 to 11
Challenge Level 
This may be used to follow on from Cubes Here and There.
Looking at the three models here you may see that they have a lot in common although they are obviously different.
The things that are the same produce the rules.
So the rules are;
$1$/ Each colour stays at the same level in each model.
$2$/ Cubes of the same colour are not separated - they stay together.
$3$/ The numbers of cubes for each colour is fixed at $1, 2, 3$ and $4$.
$4$/ The cubes sit squarely face to face with no twists or slides.
Your challenge is to create more shapes that follow the four rules.
When you have done so, compare them and show similarities and differences.
You may also like
Sponge Sections
You have been given three shapes made out of sponge: a sphere, a cylinder and a cone. Your challenge is to find out how to cut them to make different shapes for printing.
Plaiting and Braiding
This article for students gives some instructions about how to make some different braids.
Celtic Knotwork Patterns
This article for pupils gives an introduction to Celtic knotwork patterns and a feel for how you can draw them.