Skip over navigation
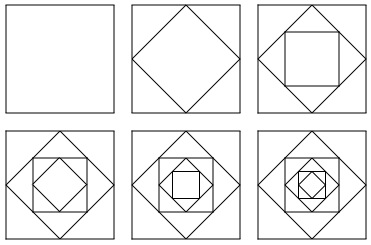 These pictures were made quite simply by starting with a square,
finding the half-way point on each side and joining those points
up. This creates a smaller shape (which also happens to be a
square) inside the original. The half-way points of this new
shape are then joined up to make a third shape. This way of making
new shapes is continued until it gets too small to do
properly.
These pictures were made quite simply by starting with a square,
finding the half-way point on each side and joining those points
up. This creates a smaller shape (which also happens to be a
square) inside the original. The half-way points of this new
shape are then joined up to make a third shape. This way of making
new shapes is continued until it gets too small to do
properly.
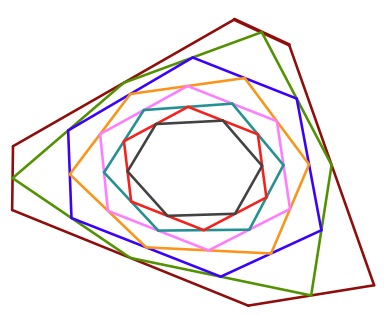
You can, of course, start with any straight-lined shape.
Here's one where I've coloured each new halving line to help to see what has happened more clearly.
So, it's your turn to have a go.
It's probably good to start with a fairly large shape since it's going to get smaller and smaller each time.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Shaping It
Age 5 to 11
Challenge Level 






You can, of course, start with any straight-lined shape.
Here's one where I've coloured each new halving line to help to see what has happened more clearly.

So, it's your turn to have a go.
It's probably good to start with a fairly large shape since it's going to get smaller and smaller each time.
Here are some challenges for you to
pursue:
- Having made a design like one above, cut out the triangles and the smallest inner shape and rearrange the pieces to form a new shape/design.
- Talk about and record the things you notice as you have drawn more and more halving lines.
- What is happening to the enclosed area each time the sides are halved? (Try investigating a regular shape first.)
This problem is based on an idea
suggested by Ian Short.
You may also like
Sports Equipment
If these balls are put on a line with each ball touching the one in front and the one behind, which arrangement makes the shortest line of balls?

