Opposite Vertices

Why do this problem?

Possible approach

These printable worksheets may be useful: Opposite Vertices - Squares
                                                             Opposite Vertices - Rhombuses
                                                             10mm Dotty Grid

You may be interested in our collection Dotty Grids - an Opportunity for Exploration, which offers a variety of starting points that can lead to geometric insights.

 

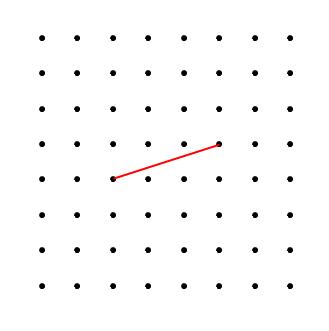
• the side of at least one square,
• the diagonal of at least one square,
• the side of at least one rhombus,
• the diagonal of at least one rhombus.

Alternatively, start by showing the image of Charlie's rubbed out squares, and give students some time to recreate the squares on dotty paper. Once they have finished, ask them to compare in pairs - have they always drawn the same square? Are there any other possibilities?
 
Bring the class together and share the techniques students were using to complete the squares.
"Draw any line you like on your dotty paper, and then try to complete a square using your line as one of the sides."
...
"Has anyone found a line that they can't use as a side of a square?" (If someone has found one, display it on the board and ask the class to help.)
"Do you think we can always draw a square using any line?"
Give students some time to discuss this and come up with justifications for their answer.
 
Next show the image of Alison's diagonals and give students time to recreate the squares.
Again, ask them to share approaches.
"Draw any line you like on your dotty paper, and then try to complete a square using your line as the diagonal."
This time, it can't always be done. If students are struggling to work out when it can and can't be done, suggest that they draw some squares and see what the diagonals have in common.
 
Then move on to rhombuses.
"Draw any line you like on your dotty paper, and then try to complete a rhombus using your line as one of the sides. How many different rhombuses can you draw using your line?"
Give students time to do this for a number of different lines of their own choosing, and then bring the class together to share their findings.
 
"When we worked on squares, there were some lines that we couldn't use as a diagonal. Will the same be true for rhombuses?"
Once again, give students time to explore.

Finally, bring the class together to share their ideas and justify their findings.
 
One technique for testing ideas at the end is to set a specific challenge, for example, to draw some lines and ask them to determine how many rhombuses could be drawn using each line as a diagonal.

Key questions

Possible support  

The interactivity in Square Coordinates helps students to visualise tilted squares.

Possible extension

Vector Journeys challenges students to explore similar relationships using vector algebra.