Skip over navigation
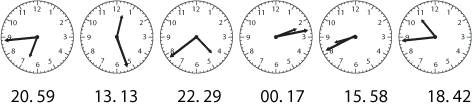
Can you put these $12$ mixed-up times in order? You could arrange them in a circle.

You can download a copy of the times on this sheet which can be printed out.
If you feel happy to try the same thing with a $24$-hour digital clock, try these $12$ times. They are on this sheet.
Suggest trying the easier related problem What's the Time?. A geared clock might also be useful to show different times. (If the clock is not geared it is much too easy to show impossible times.)


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
The Time Is ...
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The Time Is ...
Can you put these $12$ mixed-up times in order? You could arrange them in a circle.

You can download a copy of the times on this sheet which can be printed out.
If you feel happy to try the same thing with a $24$-hour digital clock, try these $12$ times. They are on this sheet.

Why do this problem?
This problem assesses and extends children's understanding of telling the time. Many children have difficulties with this, which is not surprising when you realise that analogue clocks are two dials super-imposed on one another.
Possible approach
The clock pictures and digital times can be downloaded here. These can be printed (and possibly laminated), then cut into separate cards. You could provide a set of cards for each pair, or they could be enlarged and used by a group of up to four children.
This task is probably best introduced with a minimum of teacher talk. Simply give each pair or group the cards and invite them to order the times. Give them plenty of time to tackle the challenge and try to step back. You may wish to stop them after some time to discuss what they have done so far so that ideas are shared among the whole class. This sheet of empty clock faces could be useful if children prefer to put all the times in the same format. The 24 hour clock times could be tackled by those who finish earlier than others. [Download here].
In the plenary, encourage children to explain how they went about the task, rather than only focusing on their final answer. Listen out for children who realise that the hour hand or hour digit/s is the one to look at first. If there are disagreements about the order, invite pairs or groups to try and justify their thinking. None of the times mention am/pm (in the twelve-hour version) so it
will be interesting to see how the children cope with this and whether it comes up in their conversations. This may mean that there are several different solutions to the task and this is where children's justifications of their decisions are key.
Key questions
What does that hand tell you?
Which of the clocks shows the earliest time? How do you know?
Possible extension
Learners could try the problem Two Clocks or make up their own problem cards using this sheet.
Possible support
Suggest trying the easier related problem What's the Time?. A geared clock might also be useful to show different times. (If the clock is not geared it is much too easy to show impossible times.)You may also like
In Order
Can you rank these quantities in order? You may need to find out extra information or perform some experiments to justify your rankings.
What Is the Time?
Can you put these times on the clocks in order? You might like to arrange them in a circle.

