Skip over navigation
Folding Squares
Age 14 to 16
Challenge Level 
Start with a square...
 |
 |
 |
 |
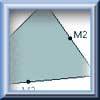
Fold to create a diagonal running from bottom left to top right. |
Find the midpoint of the base by folding. |
Fold the paper again, joining the top left corner to the midpoint of the base. |
What fractions of the diagonal do you think your new fold has created? |
Measure the two sections of the diagonal and compare their lengths.
What do you notice?
Is this what you expected?
Is this what you expected?
Can you produce a convincing mathematical argument or proof that justifies what you have found?
You might like to try A Parallelogram Trisection and Folding Fractions next.
You may also like
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
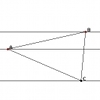
Pareq Exists
Prove that, given any three parallel lines, an equilateral triangle always exists with one vertex on each of the three lines.
The Medieval Octagon
Medieval stonemasons used a method to construct octagons using ruler and compasses... Is the octagon regular? Proof please.