Skip over navigation
An arithmagon is a polygon with numbers at its vertices which determine the numbers written on its edges. An introduction to arithmagons can be found here.
Usually, we add the numbers at the vertices to find the numbers on the edges, but these arithmagons follow a different rule.
Can you work out how the values at the vertices determine the values on the edges in the arithmagons generated by the interactivity below?
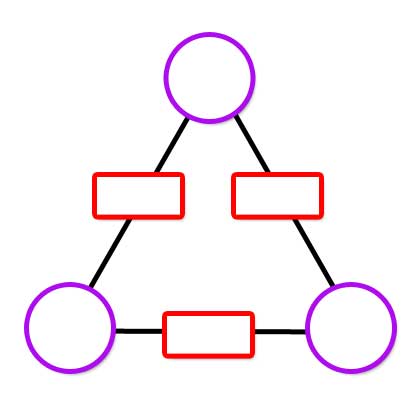
If you are given the values on the edges, can you find a way to work out what values belong at the vertices? Use the interactivity below to test out your strategies. There are three different challenge levels to try.
Once you are confident that you can work out the values at the vertices efficiently, here are some questions you might like to consider:
Can you create a multiplication arithmagon where the numbers at the vertices are all irrational but the numbers on the edges are all rational?
What about where just one or two numbers at the vertices are irrational but the numbers on the edges are rational?
Multiplication Arithmagons
Age 14 to 16
Challenge Level 
Multiplication Arithmagons printable sheet
An arithmagon is a polygon with numbers at its vertices which determine the numbers written on its edges. An introduction to arithmagons can be found here.
Usually, we add the numbers at the vertices to find the numbers on the edges, but these arithmagons follow a different rule.
Can you work out how the values at the vertices determine the values on the edges in the arithmagons generated by the interactivity below?
If you are given the values on the edges, can you find a way to work out what values belong at the vertices? Use the interactivity below to test out your strategies. There are three different challenge levels to try.
Once you are confident that you can work out the values at the vertices efficiently, here are some questions you might like to consider:
- Can you describe a strategy to work out the values at the vertices irrespective of the values given for the edges?
- Is there a relationship between the product of the values at the vertices and the product of the values on the edges?
- What happens to the numbers at the vertices if you double (or treble, or quadruple...) one or more of the numbers on the edges?
- Can you create a multiplication arithmagon with fractions at some or all of the vertices and whole numbers on the edges?
Can you create a multiplication arithmagon where the numbers at the vertices are all irrational but the numbers on the edges are all rational?
What about where just one or two numbers at the vertices are irrational but the numbers on the edges are rational?
You may also like
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Nim
Start with any number of counters in any number of piles. 2 players take it in turns to remove any number of counters from a single pile. The loser is the player who takes the last counter.
Loopy
Investigate sequences given by $a_n = \frac{1+a_{n-1}}{a_{n-2}}$ for different choices of the first two terms. Make a conjecture about the behaviour of these sequences. Can you prove your conjecture?