Walking the Squares

Thank you to everybody who sent in their solutions to this activity.

Haaniah from Woodthorpe JI School sent in this good solution:

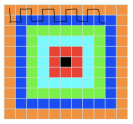
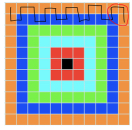
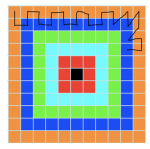
I first thought about how to get to the middle using any numbers of squares, for example, clockwise. Then I decided to go clockwise, using two squares and two rows at a time. When I got to the corner I decided to enter the corner diagonally. When I got to the final three rows, I decided to still go clockwise using two squares at a time, except this time I used three rows at a time.

  

Later she added:

First, I imagined how you could use the most number of tiles up using more than two of the same colour; you would follow it all the way around, clockwise. Then I decided to try two rows at a time for example: You start at the top right orange corner. Go right 1 then down 1, right 1 and up 1.

Continue until you reach the corner. Enter the corner diagonally then 1 across and exit diagonally as demonstrated in the picture when you have gone the whole way round enter the next rows diagonally and repeat, this time three rows at a time. When there is only three squares left, enter straight into the middle.

Swasti from Maybury Primary School, Woking also used diagonal lines to walk on as many squares as possible:

So, firstly, I worked out how many tiles the square has (121) as it would be the maximum number of tiles to walk on.
Then, I used a zig-zag pattern (as shown below) to walk on the square until I met a corner.
When I met a corner, I just realised that in order to walk on the maximum number of tiles, I couldn't use the zig-zag pattern as I did earlier because then I would have to walk on a same coloured tile more than twice.

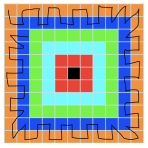
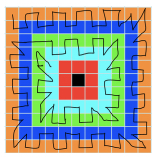
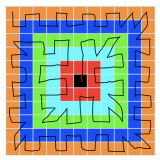
Well done to both of you for filling in all of the tiles! Have a look at Swasti's full explanation to see how she did it.

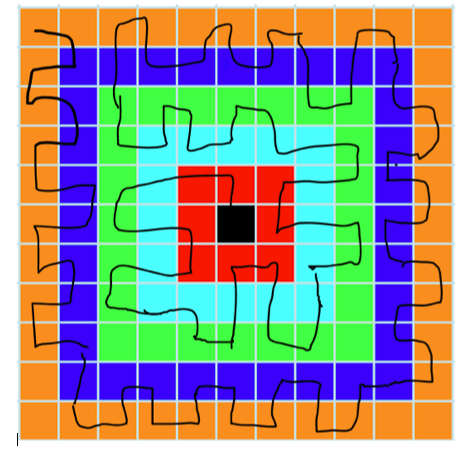
Some children didn't allow diagonal lines in their solutions. Megan from St. Oswald's Primary School managed to miss out only 10 tiles in her solution:

Daya from Brackenbury Primary School sent in these three pictures to show their progression, missing out only 9 tiles:

   

Orla from All Saints Primary School in the UK found a solution which only missed out 8 tiles:

Thank you all for sending in these pictures! I wonder if anybody can miss out fewer than 8 tiles without using any diagonal lines? If you manage this, please email us to let us know.