So It's Times!

So It's Times!

 

This activity has been particularly created for the most able. (The pupils that you come across in many classrooms just once every few years.)

 

On the table in front of you is a grid like this:-

 

 

Now imagine that you have another grid, just the same but made of plastic that you can see through.

You place the plastic one over the one on the table so that it covers it completely.

You could have flipped it over and/or turned it around as you put the plastic one down.

Then the numbers that are paired, one above the other are multiplied together.

Finally, all the results of multiplying together will be added together.

 

Without doing the $36$ multiplications and then adding them together YOUR challenge is to say which way of flipping over and/or turning the plastic grid will give you the highest total and which way will give the lowest total.

 

 

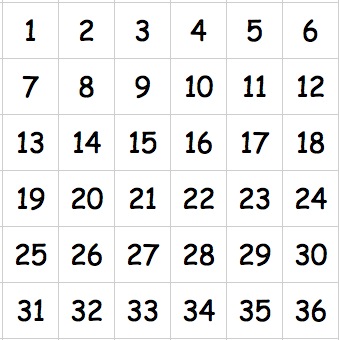
Why do this problem?

This problem is designed to challenge pupils both in number and spatial skills. It provides an opportunity for pupils to consider the properties of multiplication and to test their ideas.

Possible approach

If necessary before approaching the six by six array, present two sheets with a four by four array. Try not to go through it completely, but just try a couple of multiplications and then turn the top sheet over (or around, or both) and see what a few of the multiplications would be then.

The six by six grid can be printed out for pupils to use, and pupils might want to use tracing paper in order to create a see-through version of the grid. The challenge will need to be explained very clearly so as to prevent a lot of unnecessary calculations being made.

Key questions

Possible extension

Children could have a go at It's Times Again, which encourages children to explore how the problem changes if the numbers are no longer necessarily consecutive.