Olympic Rings

Olympic Rings

Five coloured interlocking rings have been the symbol of the Olympics for nearly one hundred years.

 

What colours can you see?

You can see the way they interlock if you click here.  

How would you describe the picture?
 
Can you design your own symbol using five coloured rings?

Other shapes could be linked in a similar way.
Have a go at linking five squares. Make them interesting colours.

 
 
 

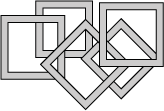
Why do this problem?

This problem is intended to get children to look really hard at something they will see many times in the next few months. It is easy to glance at something, recognise it, and not know afterwards how it really looked.

Possible approach

You could start by showing the whole group the ring design on a white-board. You can find it here.

Key questions

What can you tell me about the picture?

Possible extension

Learners could see what shapes can be linked in this way and which would not work. Alternatively, they could work out many different ways the five rings could be coloured with five colours used, and possibly draw all these combinations.

Possible support

Suggest just drawing and colouring the unjoined rings.