Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Steel Cables



Steel Cables printable worksheet
Cables can be made stronger by compacting them together in a hexagonal formation.
Here is a 'size 5' cable made up of 61 strands:
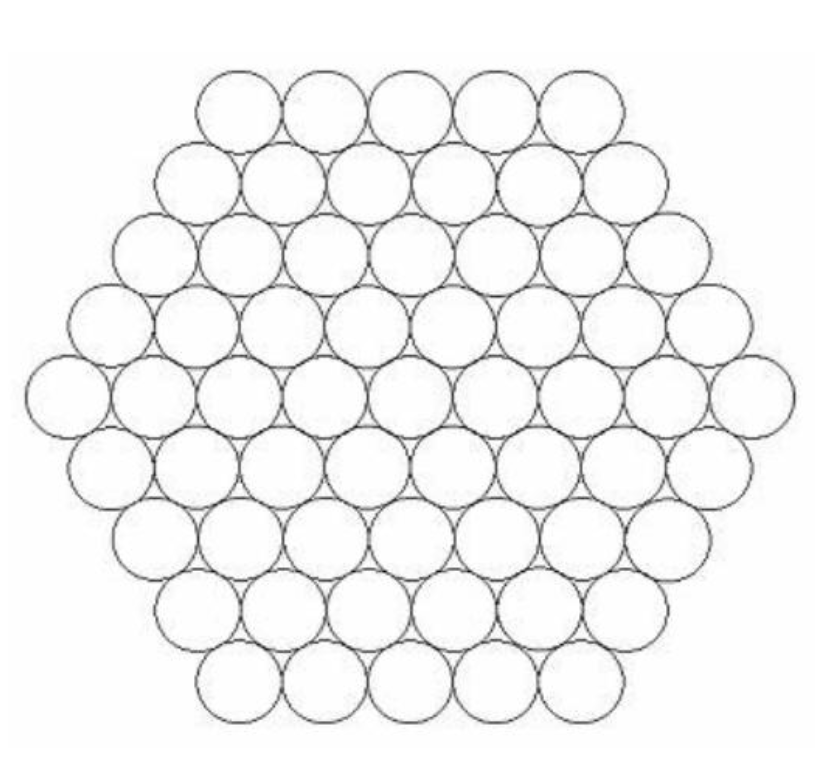
How many strands are needed for a size 10 cable?
How many for a size n cable?
Can you justify your answer?
Once you've had a go at the problem, click below to see the diagrams some students produced when they worked on it.
Do these diagrams give you any ideas for how you could work out the number of strands needed?
Group 1
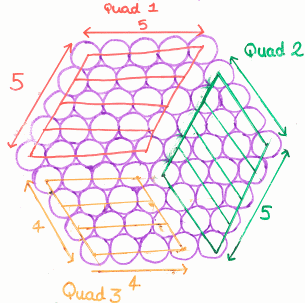
Group 2

Group 3
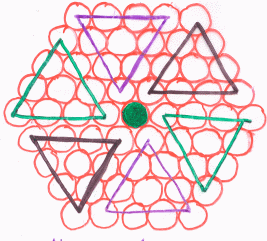
Group 4
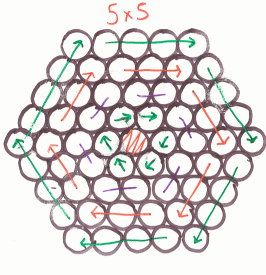
The work that these students did using their diagrams is given on the Getting Started page, if you would like another hint.
Which of the four approaches makes the most sense to you?
What do you like about your favourite approach?
Can you think of any other approaches?
Hexagonal packings are often chosen for strength or efficiency. To read more about packings, take a look at the Plus articles Mathematical Mysteries: Kepler's Conjecture and Newton and the Kissing Problem
You may also like
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...
Just Opposite
A and C are the opposite vertices of a square ABCD, and have coordinates (a,b) and (c,d), respectively. What are the coordinates of the vertices B and D? What is the area of the square?

