Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Walking Round a Triangle



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Walking Round a Triangle
This ladybird is taking a walk round a triangle. She starts off near the middle of one side of the triangle. Can you see how much she has turned when she gets back to where she started?
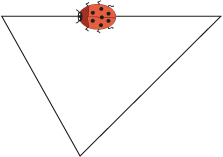
Would it be the same amount of turn if she went around another triangle?
Why?
Why do this problem?
This problem offers a geometric context for a generic proof. A generic proof works by using the structure of a particular example to show the result in the general case. In this case walking round any triangle will involve making a complete turn. A complete turn taken in three stages will always create a three stage path or a triangle.
Possible approach
Get the children to draw triangle paths on paper or in chalk on the playground. If they do this outside they can walk along the triangle path themselves. They should start by facing along one of the lines on any of the sides. It is best to start part of the way along one side so that there is no confusion about the amount of turn involved to get to the same point facing the same way. When they get back to the starting point they will have turned through a complete turn. It is important to turn in the same direction (clockwise or anticlockwise) every time.
Key questions
Which way are you facing?
How much have you turned?
How many turns are you making to go round the triangle?
How much have you turned when you get back to where you started?
Possible extension
It would be possible to look at walking round a square, a pentagon, different quadrilaterals, and so on in the same way. The problem also links to Round a Hexagon.
Possible support
More support could be offered through using a robot and programming it to go around a triangle or other polygon. The children may find it helpful to use this sheet
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?

