Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Three Neighbours



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Three Neighbours
Three Neighbours printable sheet
5, 6 and 7 are three consecutive numbers. They add up to 18.
14, 15 and 16 are also three consecutive numbers. They add up to 45.
Take other sets of three consecutive numbers and find their total.
What do you notice?
Do the totals have anything in common?
How can you be sure that what you have noticed will always be true?
Mathematicians aren't usually satisfied with a few examples to convince themselves that something is always true.
Have you been able to provide an argument that would convince mathematicians?
Liz noticed that all the totals are a multiple of 3. She found it useful to draw a picture:
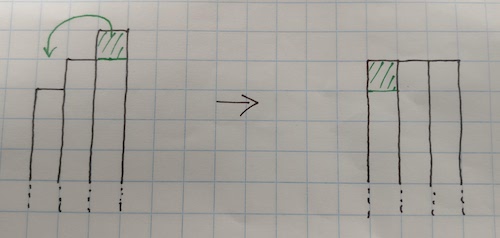
How did this help to convince Liz that three consecutive numbers always add up to a multiple of 3?
Charlie also noticed that all the totals were a multiple of 3. He thought about sets of numbers in a systematic way:
Charlie started with the three consecutive numbers 1, 2, 3. They add up to 6.
He added 1 to each, which gave him the next three consecutive numbers 2, 3, 4. They add up to 9.
He added 1 to each again, and ended up with 3, 4, 5. They add up to 12.
How did this help to convince Charlie that three consecutive numbers always add up to a multiple of 3?
What happens when you add five consecutive numbers? Seven consecutive numbers? ...
Why do this problem?
This problem provides opportunities for learners to explore three consecutive numbers, notice patterns and mathematical structures, and make and prove conjectures. Proof is a fundamental idea in mathematics and therefore this task will help you to nurture your learners as young mathematicians.
(This task can be used to support the idea of generic proof, which involves examining one example in detail to identify structures that will prove a general result. The article Take One Example, which is accompanied by video clips, unpicks generic proof in more detail.)
Possible approach
This problem featured in the NRICH Primary and Secondary webinars in January 2022.
Invite everyone to choose three consecutive numbers and add them together. Suggest that learners make a note of the three numbers and their total. You could ask them to check their partner's addition!
Ask learners to choose a different set of three consecutive numbers and add these together. Again, suggest they make a note of the numbers and their sum, and check each other's as appropriate.
At this point, begin to collate some of the sets of numbers and totals on the board, perhaps in a table with the set of three numbers in the left-hand column and their total on the same row in the right-hand column. When you have a reasonable number of examples, invite learners to talk to their partner about what they notice.
Draw together some of these noticings, writing them up on the board. At this point, encourage other members of the class to comment on and question the contributions, rather than depend on you doing the validation. Depending on the responses, and the experience of your class, you may wish to draw attention to particular noticings. For the purposes of this task, focus on the fact that the totals are all a multiple of 3. Will this always be the case?
Explain that mathematicians aren't usually satisfied with a few examples to convince themselves that something is always true. The class' challenge is to provide an argument that would convince mathematicians that the sum of three consecutive numbers is always a multiple of three. Give them time to work in pairs and, as they discuss their ideas, circulate round the room, listening out for chains of reasoning that focus on the structure of consecutive numbers, rather than on particular examples. At this point, try to provide any equipment that learners request to aid their thinking.
Bring everyone together and select a few students to share their arguments. If the examples offered in the problem have not been suggested, show Liz's approach. Allow learners time to talk to each other about how her approach would convince her that three consecutive numbers always sum to a multiple of three. Then, as a whole group, work together to build up the reasoning that would need to accompany the picture in order for it to become a proof.
In a similiar way, offer the second approach in the problem and give learners time to consider how Charlie's approach would help to convince him that this is always the case. Again, allow time to facilitate a whole group discussion during which everyone works together to create the chain of reasoning.
If your class has met algebra already, you could then offer the third approach and again, give them time to consider how this would help Claire convince herself that the sum of three consecutive numbers is always a multiple of 3.
Follow this up by asking learners to use similar reasoning to explain what happens when they add five consecutive numbers, or seven, or nine...
Key questions
What do you notice about the total?
Can you see anything in your examples that would work in exactly the same way if you used three different consecutive numbers?
Can you say what will happen every time you add any three consecutive numbers?
Can you convince your friend that this is true?
Possible support
It may be helpful to return to Two Numbers Under the Microscope if the learners are struggling with adding three numbers. This might help them to feel more comfortable with the rules they have proved in that problem and so build the foundations for this one.
Some learners may find it helpful to represent the numbers by drawing them on squared paper, or using interlocking cubes for example.
Possible extension
Some might notice that the total of three consecutive numbers is three times the middle number. Will that always be true?
You could suggest that learners try the Neighbourly Addition challenge, which focuses on adding consecutive odd numbers.
You could also ask them to explain what happens when they add four, or six, or ... consecutive numbers - see Summing Consecutive Numbers.
You may also like
Which Scripts?
There are six numbers written in five different scripts. Can you sort out which is which?

