Cracking Codes

I first developed an awareness of codes when I was nine or ten years old. We had a teacher who was extremely interested in them. Among other things he showed us the game of 'Battle Ships'. It was war-time and the idea of codes was around in the news with lots of emphasis on keeping secrets from the enemy. Although we did not know it, Alan Turing was busy working on the Enigma code at Bletchley Park.

The important aspect of a code is that it is simple for the intended recipient to read but very difficult, even impossible, for anyone not in the know. Some children at my school sent messages written in code to each other. They used a simple code in which numbers are assigned to letters (a = 1, b =2, etc) and the letters are moved along by two or three places. Thus 'cool kid' became 'fqqn mkf'.

Codes in this form can become progressively harder to crack.
For example, here is a simple coding of the first line of a well-known
nursery rhyme.

LCFM - CPT - LKNN - YGPV - WR - VJG - JKNN

As a code like this can give secrets away by the lengths of the words, it can be put into blocks of four or five letters.

LCFMC - PTLKN - NYGPV - WRVJG - JKNN

A harder version of this is to add a code word while the letters are in a numerical form and then write the changed letters. If the new number is greater than 26, subtract 26 to get the appropriate letter.

For example, to add 'baby' to 'tree top I turn each into numbers - 2.1.2.25.  and add to 20.18. 5.5. 20.15.16. letter by letter. This gives me

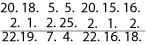
Taken back into letters this reads:  V S G D V P R.    - Enough to hush any baby!

If I add a secret word to my original nursery rhyme and turn it back into letters I get:

GBWP -  SKE - DNDI -  XYSL -  RQ - NMW - EJFQ

Put into blocks of five letters this looks like this:

GBWPS  KEDND  IXYSL   RQNMW  EJFQ

I could, of course transpose this by a few letters in either direction.

The Enigma code worked in much this way except that the letters were transposed in a much more complicated way by use of the Enigma machine.

By the way, what nursery rhyme did I use to illustrate my examples?