Skip over navigation
Cuisenaire Spirals
Age 7 to 11
Challenge Level 
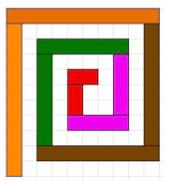
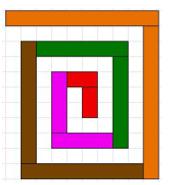
Here are two open spirals made from cuisenaire rods.
I used only the even numbered rods.
You can experiment making spirals using the rods on our Cuisenaire interactive environment.
There may be some sets of real Cuisenaire rods in your school.
You can experiment making spirals using the rods on our Cuisenaire interactive environment.
There may be some sets of real Cuisenaire rods in your school.
When you've done a lot of exploring you might like to try the something similar with numbers.
If you do, have a look at Number Spirals here.
You may also like
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Rod Fractions
Pick two rods of different colours. Given an unlimited supply of rods of each of the two colours, how can we work out what fraction the shorter rod is of the longer one?
