Skip over navigation
Article by Jenny Gage
There are a number of ways in which 3D objects can be represented on paper. Although you may be taught to use software in DT, you will also need to know how to draw by hand. Understanding the mathematical ideas which underlie the various techniques will help you to execute your drawings, as well as enabling you to make connections between geometry and a practical application of it.
There is a problem to help you explore the geometrical ideas underlying the methods of 3d drawing linked from each section.
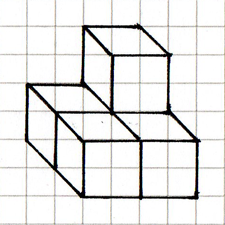
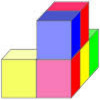
The photo below shows a multilink structure. The diagram is one way of drawing it in oblique projection, choosing the blue and yellow cubes to be the front face. Try drawing it in oblique projection, with the green and blue faces to the front. How is this diagram related to the one shown here?

Try this problem on Oblique Projection.

In an isometric drawing, all objects/lengths the same size will be drawn the same size whatever their position. In a perspective drawing two objects/lengths which are the same size will only be drawn the same size if they are equally distant from the observer.
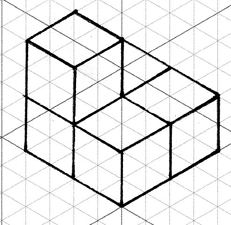
Designers and engineers often draw 3D objects in isometric perspective because objects appear in three dimensions, so the drawing gives a correct visual impression, and at the same time all distances and lengths are to scale. Typically an object will be drawn in front, top and side views, and in 3D with an isometric representation.

Try this problem on Isometric Drawing.

The most common forms of perspective drawing are one-point, two-point and three-point - this refers to the number of vanishing points, where a vanishing point is a point to which a set of lines (which were parallel in three dimensions) appear to converge.

Try this problem on linear perspective.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Age 11 to 16
Published 2012
3D Drawing
There are a number of ways in which 3D objects can be represented on paper. Although you may be taught to use software in DT, you will also need to know how to draw by hand. Understanding the mathematical ideas which underlie the various techniques will help you to execute your drawings, as well as enabling you to make connections between geometry and a practical application of it.
There is a problem to help you explore the geometrical ideas underlying the methods of 3d drawing linked from each section.
Techniques discussed in this article:
Oblique Projection
Oblique projection is based on parallel lines. If one face is chosen to be presented as it would really appear, other faces are then created by projecting rays from the given face, often at 45 degrees, creating the effect of perspective. Conventionally, oblique lines are drawn half length. More generally, the scaling of oblique lines and the angle at which they are drawn can be chosen to suit the context. If you are using squared paper, it makes sense to draw oblique lines along the diagonals of the squares and to use the diagonal of a square as a unit for the length of oblique lines, as in the drawing below.The photo below shows a multilink structure. The diagram is one way of drawing it in oblique projection, choosing the blue and yellow cubes to be the front face. Try drawing it in oblique projection, with the green and blue faces to the front. How is this diagram related to the one shown here?


Try this problem on Oblique Projection.
Isometric Perspective
The word isometric means 'equal measure' - the scale on each of the three axes is the same. This means that all objects are drawn with the correct relative proportions, so you can measure lengths on an isometric 3D drawing and know that the values you get are in the correct proportions to each other. Lengths which appear equal on an isometric drawing are equal in reality; a length which is twice another is twice that length in reality also. This is not the case for Oblique Projection - the edges of the cubes in the photo above are all the same, but are different when measured on the drawing.
In an isometric drawing, all objects/lengths the same size will be drawn the same size whatever their position. In a perspective drawing two objects/lengths which are the same size will only be drawn the same size if they are equally distant from the observer.
The diagram on the right shows a set of isometric axes. The distance between any two adjacent grid points is always equal. This means that the axes must be at 120 degrees to each other - the problem Isometric Drawing will help you to investigate this further.


Try this problem on Isometric Drawing.

Linear Perspective
We have already looked at Oblique Projection, which is one way of drawing in perspective. In this section, we will look at other methods of drawing in perspective. It is characteristic of objects drawn in perspective that more distant objects appear smaller than those close to the observer, for a given size of object, and scaling of dimensions is not constant as with isometric drawing.The most common forms of perspective drawing are one-point, two-point and three-point - this refers to the number of vanishing points, where a vanishing point is a point to which a set of lines (which were parallel in three dimensions) appear to converge.

On the drawing above, there are two vanishing points on the horizon. The diagram above right shows the detail.
Try this problem on linear perspective.
Try making a list of advantages and disadvantages for each method of drawing 3D objects discussed here. Are there particular objects which you think would be better represented by one method rather than another?
Related Collections
You may also like
Geometry and Gravity 1
This article (the first of two) contains ideas for investigations. Space-time, the curvature of space and topology are introduced with some fascinating problems to explore.
The Solid
A task which depends on members of the group working collaboratively to reach a single goal.

