Hidden Squares

Hidden Squares printable sheet

You might like to play Square It before working on this problem.

28 points have been marked on the axes below. 

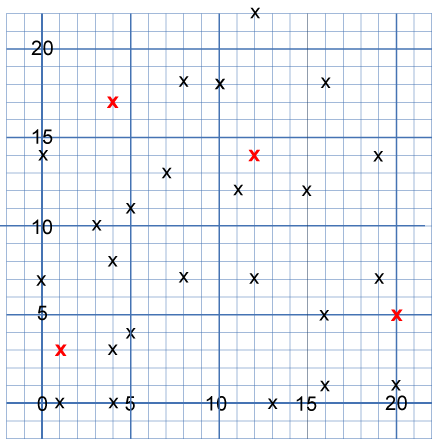
The points mark the vertices of eight hidden squares.
Each of the four red points is a vertex shared by two squares.
Each square shares exactly one vertex with another square.

Can you find the eight hidden squares?
Each square is a different size, and there are no points marked on the side of any square.



Once you've found them all, take a look at the grid below:

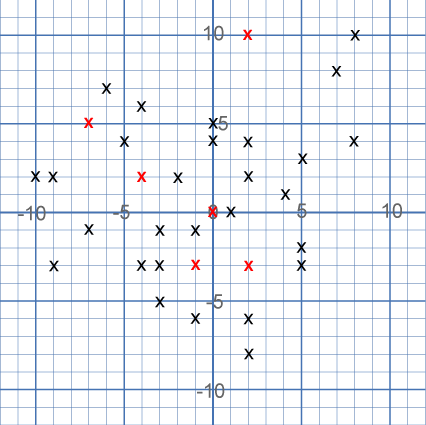
This time, there are $34$ points marking the vertices of ten hidden squares.
There are $6$ red vertices, which are shared by two squares.
All of the squares share at least one vertex with another square.

Can you find the ten hidden squares?
Once again, each square is a different size, and there are no points marked on the side of any square, although some points come very close!

Why not have another go at Square It and see if you have improved your square-spotting skills? Or take a look at Square Coordinates for a similar challenge.