Cuboid Challenge Poster
The largest volume you can make is when $x = 3\frac13$,
which gives a volume of $592\frac{16}{27}$ cm$^2$.
Why?
For any value of $x$, the other sides are each $20-2x$ and then the volume is $x\times(20-2x)\times(20-2x)$
Trying out values of $x$, a spreadsheet program like Excel is useful
| $x$ | $20-2x$ | volume | $x$ | $20-2x$ | volume | $x$ | $20-2x$ | volume | ||
| 2 | 16 | 512 | 2.5 | 15 | 562.5 | 3.1 | 13.8 | 590.36 | ||
| 3 | 14 | 588 | 3 | 14 | 588 | 3.2 | 13.6 | 591.87 | ||
| 4 | 12 | 576 | 3.5 | 13 | 591.5 | 3.3 | 13.4 | 592.55 | ||
| 5 | 10 | 500 | 3.6 | 12.8 | 589.82 | 3.4 | 13.2 | 592.42 |
You can keep going to get really close to 3.333333...
| $x$ | $20-2x$ | volume | $x$ | $20-2x$ | volume | |
| 3.31 | 13.38 | 592.571 | 3.331 | 13.338 | 592.59237 | |
| 3.32 | 13.36 | 592.585 | 3.332 | 13.336 | 592.59252 | |
| 3.33 | 13.34 | 592.592 | 3.333 | 13.334 | 592.59259 | |
| 3.34 | 13.32 | 592.591 | 3.334 | 13.332 | 592.59257 |
Using a cubic equation, the volume is $x(20-2x)^2$
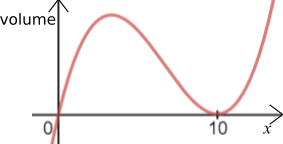
which expands to $4x^3 - 80x^2 + 400x$
Differentiate to find the stationary points:
$\frac{\text{d}V}{\text{d}x} = 12x^2 - 160x + 400$
$\begin{align} 12x^2-160x+400 &= 0\\
\Rightarrow 3x^2 - 40x + 100 &= 0\\
\Rightarrow 3x^2 - 30x -10x + 100 &= 0\\
\Rightarrow 3x(x-10) - 10(x-10)&=0\\
\Rightarrow (3x-10)(x-10)&=0\\
\Rightarrow 3x-10 = 0 \text{ or } x-10 = 0\end{align}$
$x=10$ gives the minimum area of $0$, so $3x=10\Rightarrow x=\frac{10}3$ gives the maximum area.
