Odds and Evens Made Fair
Odds and Evens Made Fair printable sheet
In the problem Odds and Evens, we introduced the following game and invited you to work out whether the game was fair:
Here is a set of numbered balls used for a game.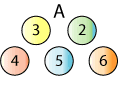 
To play the game, the balls are mixed up and two balls are randomly picked out together.
The numbers on the balls are added together.
If the total is even, you win. If the total is odd, you lose.
Can you find a set of balls where the chance of getting an even total is the same as the chance of getting an odd total?
How many sets of balls with this property can you find?
What do you notice about the number of odd and even balls in your sets?
You might like to use the Odds and Evens Interactivity to show the experimental probabilities for different sets of up to nine numbers. You can click on the purple cog to change the sets of numbers - just list the numbers you want to use, separated by a space, as in the screenshot
below:
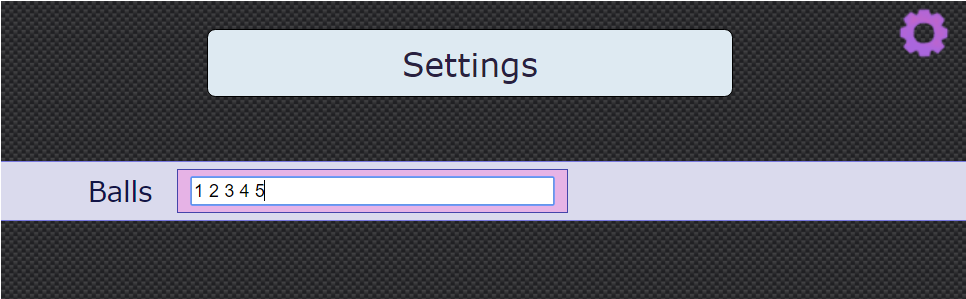
This problem featured in an NRICH video in June 2020.
Related Collections
You may also like
Coin Tossing Games
You and I play a game involving successive throws of a fair coin. Suppose I pick HH and you pick TH. The coin is thrown repeatedly until we see either two heads in a row (I win) or a tail followed by a head (you win). What is the probability that you win?
Win or Lose?
A gambler bets half the money in his pocket on the toss of a coin, winning an equal amount for a head and losing his money if the result is a tail. After 2n plays he has won exactly n times. Has he more money than he started with?
Thank Your Lucky Stars
A counter is placed in the bottom right hand corner of a grid. You toss a coin and move the star according to the following rules: ... What is the probability that you end up in the top left-hand corner of the grid?