Perimeter Possibilities
Many people must have worked really hard on this one, there were lots of detailed answers. Well done! Some people found some solutions like Alison's.
Area: 24 cm2
| Size | Perimeter |
| 4 cm x 6 cm | 20 cm |
| 3 cm x 8 cm | 22 cm |
| 2 cm x 12 cm | 28 cm |
| 1 cm x 24 cm | 50 cm |
A key idea is that you can use fractions or decimals to get more solutions. Alison found one more for us, and Patrick found a few extra too.
| 1.5 cm x 16 cm | 35 cm |
| 0.5 cm x 48 cm | 97 cm |
| 0.25 cm x 96 cm | 192.5 cm |
Notice that we can get an odd number for the perimeter in more than one way, and even find a fractional perimeter. Thomas and Zaki made a great observation.
There are infinitely many perimeters you can make with an area of 24 as you
can keep on multiplying the length by 2 and dividing the width by 2 so the
perimeter keeps getting bigger.
Raadiyah realised that you could divide by numbers other than 2 to find the following.
| 0.000001 cm x 24000000 cm | 48000000.000002 cm |
| 0.0000001 cm x 240000000 cm | 480000000.0000002 cm |
Amy had a great idea for finding a small perimeter using square roots. The square root of 24 is not even expressible as a fraction or a finite decimal, it is irrational!
To get the smallest possible perimeter it needs to be a square so I found the square root of 24 which was approximately 4.898979486.
| $\sqrt{24}$ cm x $\sqrt{24}$ cm | $4\times \sqrt{24}$ cm |
| 4.898979486 cm x 4.898979486cm | 19.59591794 cm |
If you know how to plot tricky graphs and how to find the solution to simultaneous equations you might like to think about how to make any possible perimeter.
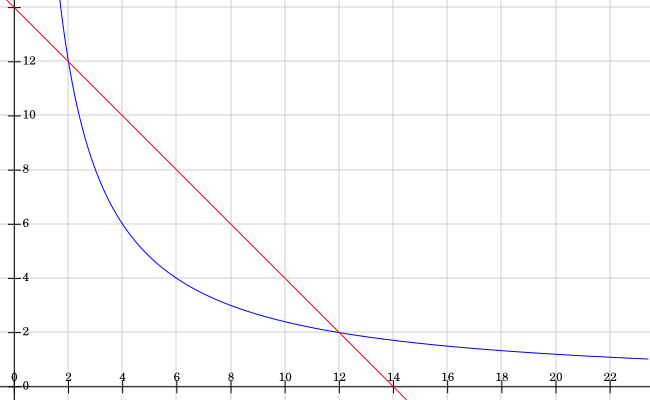
I've plotted the graphs 2x+2y=28 in red and xy=24 in blue. Where do the lines intersect? What does this tell us about the possible rectangles?
Related Collections
You may also like
Framed
Seven small rectangular pictures have one inch wide frames. The frames are removed and the pictures are fitted together like a jigsaw to make a rectangle of length 12 inches. Find the dimensions of the pictures.
Tilted Squares
It's easy to work out the areas of most squares that we meet, but what if they were tilted?
Four or Five
The diagram shows a large rectangle composed of 9 smaller rectangles. If each of these rectangles has integer sides, what could the area of the large rectangle be?