School Fair Necklaces

We had a number of solutions sent in.  Most treated the bracelets as being in a straight line rather than in a circle, which can make it more difficult to check whether you are duplicating ones already found.

We had the following from Lyneham Primary Junior Maths Challenge Group in Australia:

On Friday we worked on the necklaces problem in our maths group.
We used some different coloured counting blocks (unifix) to make symmetrical patterns of eight blocks with two colours.
We figured out that with those blocks we could make six different combinations that were symmetrical (see picture). And then we figured out that it didn't matter if you cut half of it off because they are symmetrical, so the halves are exactly the same.
We found six different towers of four blocks, two of each colour (see at the bottom of the photo). So therefore there are six possible ways you can do it.




We also heard from Cole and Sachi at Randlay Primary School:

I used O,G,G,O,O,G,G,O* for number one.
For number two we did O,G,O,G,G,O,G,O.
Number three: G,O,G,O,O,G,O,G.
Number four we did O,O,G,G,G,G,O,O.
Number five: G,G,O,O,O,O,G,G.
*O stands for orange and G stands for green.
We found over five ways to do the challenge that were different and symmetrical with the same colour.

I wonder whether you can see the sixth way that you've missed out?

Lara-Jade at Bay Primary School wrote:

I started with nine beads and worked out that because it has to be symmetrical the bead at the bottom must be of one colour because the clue says four beads of one colour and five beads of the other colour. So I thought yellow could be at the bottom and my pattern was:
Y,G,Y,G,(Y),G,Y,G,Y.
Then I worked out 13 beads. I thought because it is another odd number the bead at the bottom must be the colour of bead with the most in it. So I worked out the pattern which was
Y,G,Y,G,Y,G,(Y),G,Y,G,Y,G,Y.
Then I tried to work out what 10 was. Then I tried it and thought that it wouldn't work because it was even but I was wrong. So I tried it again and got the pattern right which was:
Y,G,Y,G,(Y)(Y),G,Y,G,Y.
I then moved onto 12. Because 10 worked 12 MUST work so I worked out the pattern which was: Y,G,Y,G,Y,(G)(G),Y,G,Y,G,Y.
Finally, I did 11 beads. And worked out the pattern which was:
G,Y,G,Y,G,(Y),G,Y,G,Y,G.

We had an email sent in from a teacher in Oregon U.S.A. saying:

My students at Springwater Environmental Sciences School found there were zero combinations that worked if you used 5 beads of each colour. I have attached a few explanations.

   
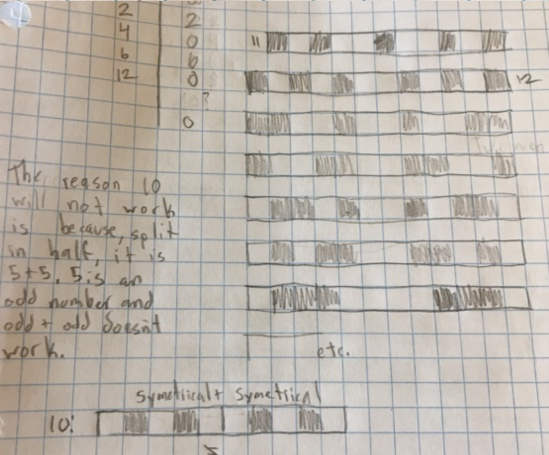
The teacher later added :-
We spent two class periods looking for a pattern, but could not find one.
One of my students realized that odds and evens should be treated differently, and as a class, we found that multiples of 4 always work, but could not find a pattern of how they increased as you added more beads.
One student had a great idea to start with smaller numbers of beads and work up from there to see the pattern, so we started with one bead but we always either had equal or only one more bead than the other colour.
This task was a great follow up to the three colour block tower (https://nrich.maths.org/137) because the symmetry aspect really changed up the thinking. 

Thank you, this was a later solution that was emailed in which dealt very well with the situation when having 10 beads and 5 of each colour. Well done!

Did you find any other ways of making symmetrical necklaces, I wonder? Is there anything general you could say about even and odd numbers of beads?
It's interesting to see the different ways of recording thinking - some of you using cubes, some of you using letters and some of you using squared paper.

If you have worked on this activity, then do send us your thoughts too.