Skip over navigation
Perimeter and Area
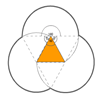
Curvy Areas
Age 14 to 16
Challenge Level 
This problem offers students the opportunity to calculate areas of parts of circles and use $\pi$ in calculations.
Triangles and Petals
Age 14 to 16
Challenge Level
This problem offers the opportunity to practise calculating arc lengths, working in terms of $\pi$, and calculating interior angles of regular polygons
Track Design
Age 14 to 16
Challenge Level
This problem offers an authentic context within which to calculate arc lengths and requires students to present their findings in a convincing manner.
Salinon
Age 14 to 16
Challenge Level
This shape comprises four semi-circles. What is the relationship between the area of the shaded region and the area of the circle on AB as diameter?
Arclets
Age 14 to 16
Challenge Level
Each of the following shapes is made from arcs of a circle of radius r. What is the perimeter of a shape with 3, 4, 5 and n "nodes".