Who Is Cheating?

This problem is part of the Great Expectations: Probability through Problems collection. It is designed for classroom use; see the Teachers' Resources for a suggested classroom approach.


You can investigate this question through a practical experiment.
You will need a die with four blue faces and two red faces, two ordinary numbered dice, and some red, blue, green and yellow multi-link cubes.  (If you do not have a die with coloured faces, use a numbered die and designate 1, 2, 3 and 4 to be blue and 5, 6 to be red).

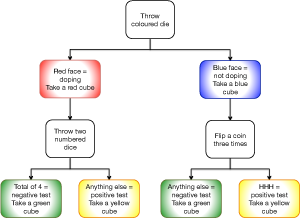
First, investigate what happens for one athlete.

Rules for the simulation:

1. Throw the coloured die.
   • If it is red, the athlete is taking the banned substance.  Take a red cube.
   • If it is blue, the athlete is not taking the banned substance.  Take a blue cube.
2. If the athlete is taking a banned substance , throw two numbered dice.
   • If the sum of the two dice is 4 the athlete tests negative - take a green cube.
   • Anything else means they test positive - take a yellow cube.
3. If the athlete is not taking a banned substance, flip a coin three times.
   • Three heads means they test positive - take a yellow cube.
   • Anything else means they test negative - take a green cube.

This simulation is summarised in the flow chart.

Stick your two cubes together.

What do each of these mean?

• red and yellow
• blue and yellow
• red and green
• blue and green

Now repeat the experiment 36 times in total, so that you have 36 pairs of cubes.

Are you surprised by your results?

How do they compare with what we would expect?  
This worksheet will help you to work out the expected results.  You need to be sure that you have correctly identified how many possible outcomes there at each stage, and how many of those give each result - this Sample Space worksheet will help you with that.

Here are some questions to consider:
What can you say about the proportion of false positives (that is, athletes who test positive even though they have not taken the banned substance)?

Given that an athlete is not taking the banned substance, what is the probability that they test positive?

What can you say about the proportion of false negatives (that is, athletes who test negative even though they have taken the banned substance)?

Given that an athlete is taking the banned substance, what is the probability that the test is negative?  (What figure should go in the denominator here?)

This worksheet will help you to interpret the expected results as probabilities, leading to a general result for probability trees - the multiplication rule.

Extension questions

For these questions, you will need to identify carefully which set of athletes the question is asking you about, in order to identify which number should go in the denominator - they are not all the same!

• What is the probability that an athlete, chosen at random, receives a false positive result?
• Given that an athlete was not taking the banned substance, what is the probability that their test result is positive?
• Given that an athlete receives a positive test, what is the probability that they were not in fact taking the banned substance?

Which representation is most helpful in answering these questions?
Why?

Rules for the simulation:

1. Throw the coloured die.
   • If it is red, the athlete is taking the banned substance.  Take a red cube.
   • If it is blue, the athlete is not taking the banned substance.  Take a blue cube.
2. If the athlete is taking a banned substance (you have a red cube), throw two numbered dice.
   • If the total on the two dice is 4 (ie. 1+3, 3+1, 2+2) that means a negative test result - take a green cube.
   • Anything else means a positive test result - take a yellow cube.
3. If the athlete is not taking a banned substance (you have a blue cube), flip a coin three times.
   • Three heads means a positive test result - take a yellow cube.
   • Anything else means a negative test result - take a green cube.