A Brief Introduction to the Argand Diagram

This problem follows on from A Brief Introduction to Complex Numbers

Watch the video below to learn about the Argand diagram.

If you can't see the video, reveal the hidden text which describes the video

Complex numbers can be represented on an Argand diagram. The real part of a number corresponds to the $x$ coordinate and the imaginary part of a number corresponds to the $y$ coordinate. So the number $z=x+iy$ would be represented by the point $(x,y)$.
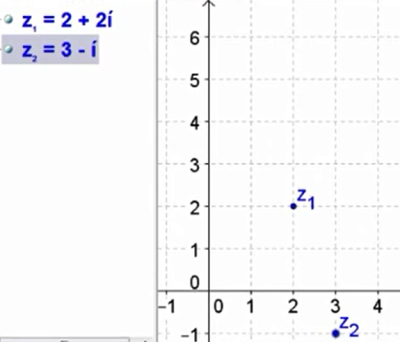
The Argand diagram below shows the numbers $z_1=2+2i$ and $z_2=3-i$.

You can explore the Argand diagram using GeoGebra, a free-to-download graphing package.
We have created an online GeoGebra worksheet for you to explore the questions below.




Let $z_1$ and $z_2$ be complex numbers represented on an Argand diagram, and let $z_3$ be their product.

Fix $z_1$, and move $z_2$ until $z_3$ is on the x-axis.

What can you say about the trajectory of $z_2$ as you move it to keep $z_3$ on the x-axis?

Repeat the above for other values of $z_1$, keeping a record of the values of $z_2$ and $z_3$.

• In each case, can you make predictions about where $z_2$ needs to be for $z_3$ to be on the x-axis?
• Can you predict where $z_2$ needs to be when you want $z_3$ to be at a given point on the x-axis?

Can you use algebra to explain why the values of $z_2$ you found for each $z_1$ give real values for $z_3$?


Now carry out the same process but this time aiming to keep $z_3$ on the y-axis.

You may want to have a go at Complex Squares next.