Skip over navigation
Two children stand on different tiles, and hold a ribbon or ribbons across the pool.
Each child can hold one or two ribbons at a time.
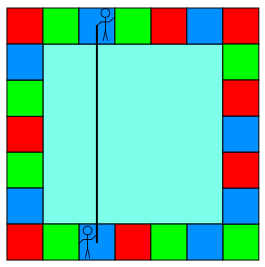
Each ribbon runs from the middle of the tile that the child is standing on.
The children are trying to make squares with their ribbons that they call 'ribbon squares'.
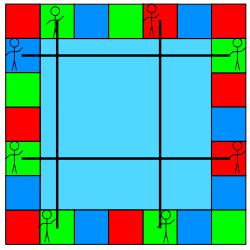
Here's a ribbon square they made. It has an area of 9 square tiles.
What are the smallest and largest ribbon squares they can make?
How many differently sized ribbon squares can they make?
What happens if the square swimming pool is made from 20 tiles?
How many ribbon squares can they make then?
This problem featured in a preliminary round of the Young Mathematicians' Award.
The activity also opens out the possibility of pupils asking “I wonder what would happen if . . .?” Pupils' curiosity may be easily aroused while finding solutions to the challenges.
Ribbon Squares
Age 7 to 11
Challenge Level 
Ribbon Squares
Imagine a square swimming pool with 24 single tiles around it, like the one in the diagram.Two children stand on different tiles, and hold a ribbon or ribbons across the pool.
Each child can hold one or two ribbons at a time.
Each ribbon runs from the middle of the tile that the child is standing on.
The children are trying to make squares with their ribbons that they call 'ribbon squares'.
Here's a ribbon square they made. It has an area of 9 square tiles.
How many differently sized ribbon squares can they make?
What happens if the square swimming pool is made from 20 tiles?
How many ribbon squares can they make then?
This problem featured in a preliminary round of the Young Mathematicians' Award.
Why do this problem?
This problem gives pupils a challenge in both spatial and numerical problem solving. It is also quite a challenge for recording methods. It is probably best suited for a group of children who are confident problem solvers.The activity also opens out the possibility of pupils asking “I wonder what would happen if . . .?” Pupils' curiosity may be easily aroused while finding solutions to the challenges.
Possible approach
It would be good to have a square grid background and then have coloured squares arranged for the tile surround.
This could be on card on the floor for the children to see, or represented on an interactive whiteboard.
Some time needs to be spent arranging ribbons/string/lines that obey the rules and produce a square so that learners can internalise the rules.
Give children time to explore for themselves and intersperse this with some 'mini plenaries' to exchange ideas.
It may be helpful for learners to have a printed copy of the task.
This could be on card on the floor for the children to see, or represented on an interactive whiteboard.
Some time needs to be spent arranging ribbons/string/lines that obey the rules and produce a square so that learners can internalise the rules.
Give children time to explore for themselves and intersperse this with some 'mini plenaries' to exchange ideas.
It may be helpful for learners to have a printed copy of the task.
Key questions
How are you working out the area to show they are not the same?
How have you decided that this is the biggest/smallest?
How have you decided that this is the biggest/smallest?
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
Tiles on a Patio
How many ways can you find of tiling the square patio, using square tiles of different sizes?
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?