Skip over navigation


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
How Much?
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
How Much?
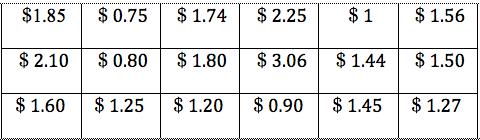
Dan bought a packet of crisps and an ice cream.
The cost of both of them together is in one of the boxes below.

Use these clues to find out how much he paid:
1. You need more than three coins to make this amount.
2. There would be change from the most valuable coin.
3. The crisps cost more than $0.50.
4. The ice cream costs exactly twice as much as the crisps.
Why do this problem?
This problem requires children to work systematically and makes an interesting context for practising arithmetic in the context of money.
Possible approach
In order to get children thinking about money, you could use a variation of the Buying a Balloon problem as a starter activity. You might want to limit the number of coins to four rather than six, for example, so there are fewer possibilities. However in this instance, the purpose of this initial task would be
to remind children of all the different coins, rather than to make sure they had all possible combinations.
To introduce the main activity, you could have the problem up on the board to start with and read through the clues as a class. Discuss which clues might be immediately useful and which might have to be left for a while. Leave children to have a go at the problem in pairs - they might find it helpful to have this sheet ( .pdf .doc) between two. Emphasise that you'll be interested in knowing how they tackled the problem during the plenary. Once they have been working for a few minutes, stop them to talk about how they are recording their thinking. Share good suggestions
with the class (for example, crossing out numbers which can be ruled out).
In a plenary, focus on asking some children to explain the order in which they used the clues. Use this to highlight the fact that there isn't necessarily one right way to approach this problem and that just because a piece of information is written first, it doesn't mean it can be used first! If there are any children who have tried the extension idea, you could also use one of their
problems for the whole class to try.
Key questions
Which clue could we use first?
Are there any numbers that we can discount using that information?
Possible extension
You could challenge children to make their own sets of clues based on the same amounts of money and even amounts of their choice.
Possible support
It might be helpful for children to have cut out cards with the sums of money written on (or larger versions printed from the problem sheet). This way, they can move the cards into "possible" and "not possible" piles which are easily altered and might therefore be less threatening. It might be a good idea to try One of Thirty Six first.
You may also like
Christmas Shopping
Vera is shopping at a market with these coins in her purse. Which things could she give exactly the right amount for?
Buying a Balloon
Lolla bought a balloon at the circus. She gave the clown six coins to pay for it. What could Lolla have paid for the balloon?


