Skip over navigation


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Circular Circuitry
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
All credit to Alex Bramham, for this excellent and complete solution;
Each wire can be either on or off. Wires that must be the same have been assigned the same variable. The variables are 1 when the wire is on, and 0 when off. Relationships between these variables model the circuit.
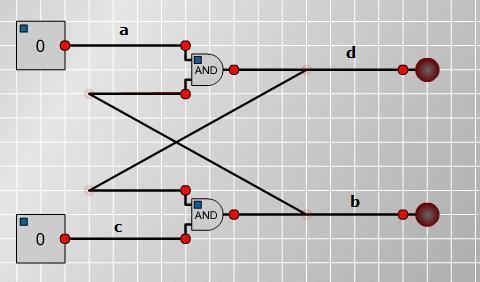
Circuit 1

The AND comparison can be modelled as returning a value equal
to the product of the two compared wires. This is because the
product is $1$ when both are on $1$ and $0$ otherwise.
$d$ is the result of an AND comparison of $a$ and $b$. $d =
ab$. $b$ is the result of an AND comparison of $c$ and $d$, $b =
cd$.
This can be substituted into the first equation: $d = acd$,
$acd - d = 0$, $d(ac-1) = 0$. And the first can be substituted into
the second: $b = abc$, $abc - b = 0$, $b(ac-1) = 0$, $ac-1$ only
equals zero when both $a$ and $c$ are $1$, so unless this is the
case, $b$ and $d$ will both be off. When $a$ and $c$ are both $1$,
the equations simplify to $b = d$, and nothing further can be
deduced about the lamps, other than that they are the same.
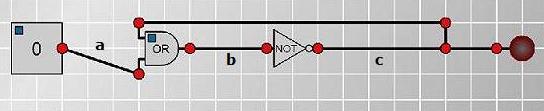
Circuit 2

The OR comparison returns zero when both values are zero,
otherwise it returns one. Subtracting the product from the sum can
be used to model this, as it returns zero when the values are zero
and one otherwise.
The NOT function returns one for zero and zero for one.
Subtracting the value from one models this.
$b$ is the result of an OR comparison of $a$ and $c$, $b = a +
c - ac$, $c$ is a NOT function for $b$, $c = 1 - b$ This can be
substituted into the first equation: $b = a + 1 - b - a(1-b), b = a
+ 1 - b -a + ab$ $b = 1 - b + ab$, $2b - ab = 1$, $b(2-a) = 1$. So
$b = 1$ and $a = 1$. If $b = 1$, equation two gives $c = 0$, and
then equation one makes $a = 1$. Conversely, if $a = 1$, equation
one makes $b = 1$, and equation two makes $c = 0$. So there is a
unique solution, the switch must be on, and the lamp is off.
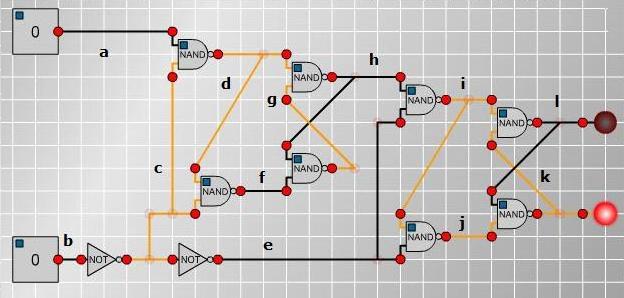
Circuit 3

The NAND comparison returns one, unless the two values are
both one. Subtracting the product from one models this. Every NAND
comparison expressed as an equation involving the values it
compares and the result is as follows:
$d = 1 - ac$
$f = 1 - cd$
$h = 1 - dg$
$g = 1 - fh$
$i = 1 - eh$
$j = 1 - ei$
$k = 1 - jL$
$L = 1 - ik$
The NOT functions:
$c = 1 - b$
$e = 1 - c$
If $b = 1$, then $c = 0$ and $e = 1$, the first two equations
would make $d = 1$ and $f = 1$. The last three equations become: $j
= 1 - i$, $k = 1 - jL$, $l = 1 - ik$ Subbing $j$ and $L$ into $k$
gives $k = 1 - (1-i)(1-ik)$, $k = 1 - (1-i-ik+iik)$, $k =
1-1+i+ik-iik$, $k = i + ik - iik$, $k = i$, $L = k$
Note: $1$ or $0$ squared is still the same value, so $ii$ can
be replaced with $i$. $ik$ and $l$ can be replaced by $i$ in the
last equation: $L = 1 - ik$, $i = 1 - i$, $2i = 1$. Which is not
true for either $0$ or $1$.
A contradiction means that $b$ cannot equal $1$. Now that $b =
0$ is known, the original equations can be updated:
$c = 1 - b, c = 1$
$e = 1 - c, e = 0$
$d = 1 - a$
$f = 1 - d$
$h = 1 - dg$
$g = 1 - fh$
$i = 1$
$j = 1$
$k = 1 - jL$
$L = 1 - ik$
And again with the values of $i$ and $j$: $k = 1 - L$, $L= 1 -
k$
So now all the known information is:
$b = 0$
$c = 1$
$e = 0$
$i = 1$
$j = 1$
$d = 1 - a$
$f = 1 - d$
$h = 1 - dg$
$g = 1 - fh$
$L = 1 - k$
If $a = 0$, then $d = 1$, $f = 0$, $g = 0$, $h = 1$.
If $a = 1$, then $d = 0$, $f = 1$, $h = 1$, $g = 0.$ (By
looking at the last five equations in order). So $g = 0$ and $h =
1$.
The solution is:
$b = 0$
$c = 1$
$e = 0$
$g = 0$
$h = 1$
$i = 1$
$j = 1$
$d = 1 - a$
$f = 1 - d$
$L = 1 - k$
No more information can be derived.
Conclusion: switch $b$ must be off, switch $a$ does not affect
the lamps, though it can be on or off, and exactly one lamp will
always light, either one is possible.
It is not valid to consider what would happen when switch $b$
is "flicked on and then flicked off" because if $b$ is on there is
a contradiction caused and some wires would be neither on nor off.
If switch $a$ was flicked on and off, $i$ and $j$ would remain
active, and hence no change to the end part of the circuit.
You may also like
Impuzzable
This is about a fiendishly difficult jigsaw and how to solve it using a computer program.
A Computer Program to Find Magic Squares
This follows up the 'magic Squares for Special Occasions' article which tells you you to create a 4by4 magicsquare with a special date on the top line using no negative numbers and no repeats.

