Curved Square
A square of side length 1 has an arc of radius 1 drawn from each of its corners, as in the following diagram. The arcs intersect inside the square at four points, to create the shaded region.
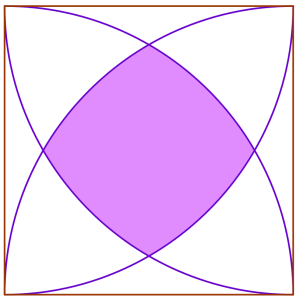
What is the area of the largest square that can be completely contained within the shaded region?
Is this a good estimate of the actual shaded area?
What is the exact area of the central shaded region?
How did that compare to your estimate?
Can you find more than one method to work out the exact area?
Click here for a poster of this problem.
You may also like
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Orthogonal Circle
Given any three non intersecting circles in the plane find another circle or straight line which cuts all three circles orthogonally.
Ellipses
Here is a pattern for you to experiment with using graph drawing software. Find the equations of the graphs in the pattern.