Skip over navigation
This printable worksheet may be useful: Isosceles Triangles.
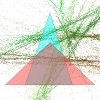
Show the class this triangle and ask them to list as many properties of the triangle as they can.
Group students into threes or fours.
Ask them to find some triangles that satisfy the following criteria:
• It is an isosceles triangle.
• The area is 9 square centimetres.
• Each vertex has whole number coordinates.
• One of the vertices is at (20, 20).
Once students have found a few examples, you may wish to use the interactive applet in the problem to check their work. Then challenge them to find all the possible triangles that satisfy the four conditions.
Make it clear that you will expect them to justify that they have found all possibilities.
Once groups feel that they have finished, they could try to explain clearly to the class why they are convinced they have found all of the solutions. Those who missed out solutions could be encouraged to think about why these solutions were overlooked.Key questions
Instead of using (20,20) as the coordinates of one of the vertices, you could use (10,10), and encourage students to draw the different possibilities on a coordinate grid (perhaps with (10,10) marked on it).
Isosceles Triangles
Age 11 to 14
Challenge Level 
Why do this problem?
Paul Andrews, a respected mathematics educator based at Cambridge University, explains why he likes this problem :
"I first saw it used as a homework question more than ten years ago with a year seven class (11 year old students) in Budapest and have used it with every group I have taught since - initial teacher training, mathematics education research students, in-service; everyone gets it.
I love it because it forces an acknowledgement of so many different topics in mathematics and is sufficiently challenging to keep almost any group meaningfully occupied within a framework of Key Stage Three mathematics content. This, for me, is the key to a good problem; Key Stage Three content alongside non-standard and unexpected outcomes.
For example, notwithstanding the obvious problem solving skills necessary for managing such a non-standard problem, I think it requires an understanding of coordinates, isosceles triangles and the area of a triangle. It requires an awareness of the different factors of 18 and which are likely to yield productive solutions. It requires, also, an understanding not only of basic transformations like reflection and rotation but also an awareness of their symmetries. Moreover, the solution, which is numerically quite small, is attainable without being trivial.
In short, I love this problem because of the wealth of basic ideas it encapsulates and the sheer joy it brings to problem solvers, of whatever age, when they see why the answer has to be as it is. It is truly the best problem ever and can provoke some interesting extensions."
I love it because it forces an acknowledgement of so many different topics in mathematics and is sufficiently challenging to keep almost any group meaningfully occupied within a framework of Key Stage Three mathematics content. This, for me, is the key to a good problem; Key Stage Three content alongside non-standard and unexpected outcomes.
For example, notwithstanding the obvious problem solving skills necessary for managing such a non-standard problem, I think it requires an understanding of coordinates, isosceles triangles and the area of a triangle. It requires an awareness of the different factors of 18 and which are likely to yield productive solutions. It requires, also, an understanding not only of basic transformations like reflection and rotation but also an awareness of their symmetries. Moreover, the solution, which is numerically quite small, is attainable without being trivial.
In short, I love this problem because of the wealth of basic ideas it encapsulates and the sheer joy it brings to problem solvers, of whatever age, when they see why the answer has to be as it is. It is truly the best problem ever and can provoke some interesting extensions."
Possible approach
This printable worksheet may be useful: Isosceles Triangles.
Show the class this triangle and ask them to list as many properties of the triangle as they can.
Group students into threes or fours.
Ask them to find some triangles that satisfy the following criteria:
• It is an isosceles triangle.
• The area is 9 square centimetres.
• Each vertex has whole number coordinates.
• One of the vertices is at (20, 20).
Once students have found a few examples, you may wish to use the interactive applet in the problem to check their work. Then challenge them to find all the possible triangles that satisfy the four conditions.
Make it clear that you will expect them to justify that they have found all possibilities.
Once groups feel that they have finished, they could try to explain clearly to the class why they are convinced they have found all of the solutions. Those who missed out solutions could be encouraged to think about why these solutions were overlooked.Key questions
- How do you know that your triangles have the correct area?
- Are there any more like that?
- Can you explain why you are certain that there are no more solutions?
Possible support
Instead of using (20,20) as the coordinates of one of the vertices, you could use (10,10), and encourage students to draw the different possibilities on a coordinate grid (perhaps with (10,10) marked on it).
Possible extension
Challenge students to find a general method for working out how many different isosceles triangles can be drawn for any given area (assuming we retain all the other constraints).
The problem doesn't insist that one edge is horizontal/vertical - are there any triangles with no horizontal or vertical sides that satisfy the criteria?
Related Collections
You may also like
Isosceles
Prove that a triangle with sides of length 5, 5 and 6 has the same area as a triangle with sides of length 5, 5 and 8. Find other pairs of non-congruent isosceles triangles which have equal areas.
Linkage
Four rods, two of length a and two of length b, are linked to form a kite. The linkage is moveable so that the angles change. What is the maximum area of the kite?