Skip over navigation
Article by NRICH team
Magic Squares are square grids with a special arrangement of numbers in them. These numbers are special because every row, column and diagonal adds up to the same number. So for the example below, 15 is the magic number. Could you work this out just from knowing that the square uses the numbers from 1 to 9?

Also, the two numbers that are opposite each other across the centre number will add up to the same number. So in the square above, 8 + 2 = 10 , 6 + 4 = 10, 1 + 9 = 10 and 3 + 7 = 10. Why is this?
The "order" of a magic square tells how many rows or columns it has. So a square with 3 rows and columns is Order 3, and a square with 4 rows and columns is Order 4 and so on. If you'd like to find out more about how to make up your own magic squares, and the mathematics behind it all, you can go to some other pages on the website such as Magic Squares and Magic Squares II .
So the numbers in the Magic Square are special, but why are they called magic? It seems that from ancient times they were connected with the supernatural and magical world. The earliest record of magic squares is from China in about 2200 BC. and is called "Lo-Shu". There's a legend that says that the Emperor Yu saw this magic square on the back of a divine tortoise in the Yellow River.
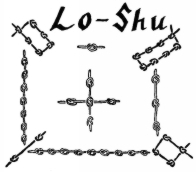 The black knots show even numbers and the white knots show odd numbers. Look closely and you'll see that this ancient magic square is the same as our example above. Magic squares were first mentioned in the Western world in the work of Theon of Smyrna. They were also used by Arab astrologers in the 9th century to help work out horoscopes. The work of the Greek mathematician Moschopoulos in 1300
A.D. help to spread knowledge about magic squares. So here we are now, more than 700 years later, and teachers are using them in class for problem solving and practising addition.
The black knots show even numbers and the white knots show odd numbers. Look closely and you'll see that this ancient magic square is the same as our example above. Magic squares were first mentioned in the Western world in the work of Theon of Smyrna. They were also used by Arab astrologers in the 9th century to help work out horoscopes. The work of the Greek mathematician Moschopoulos in 1300
A.D. help to spread knowledge about magic squares. So here we are now, more than 700 years later, and teachers are using them in class for problem solving and practising addition.
You can make similar magic squares, of order 3, using different numbers. Can you see any patterns in the numbers that work?
Reference:
The Joy of Mathematics by T. Pappas

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Age 7 to 16
Published 2000 Revised 2019
An Introduction to Magic Squares
Magic Squares are square grids with a special arrangement of numbers in them. These numbers are special because every row, column and diagonal adds up to the same number. So for the example below, 15 is the magic number. Could you work this out just from knowing that the square uses the numbers from 1 to 9?

Also, the two numbers that are opposite each other across the centre number will add up to the same number. So in the square above, 8 + 2 = 10 , 6 + 4 = 10, 1 + 9 = 10 and 3 + 7 = 10. Why is this?
The "order" of a magic square tells how many rows or columns it has. So a square with 3 rows and columns is Order 3, and a square with 4 rows and columns is Order 4 and so on. If you'd like to find out more about how to make up your own magic squares, and the mathematics behind it all, you can go to some other pages on the website such as Magic Squares and Magic Squares II .
But why are they called magic?
So the numbers in the Magic Square are special, but why are they called magic? It seems that from ancient times they were connected with the supernatural and magical world. The earliest record of magic squares is from China in about 2200 BC. and is called "Lo-Shu". There's a legend that says that the Emperor Yu saw this magic square on the back of a divine tortoise in the Yellow River.

You can make similar magic squares, of order 3, using different numbers. Can you see any patterns in the numbers that work?
Reference:
The Joy of Mathematics by T. Pappas
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.

