Poly Plug Rectangles

Thank you to everybody who sent us their ideas about how to find the monkey's rectangle. You can see some videos of children working on this task in our Early Years Children's Thinking section.

Sion from Twyford School in England sent in this strategy:

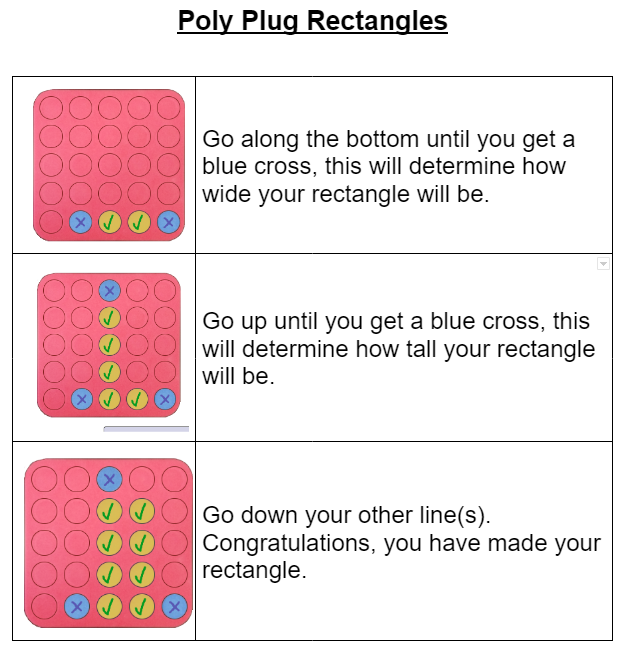
Well done, Sion - I agree that this strategy will always work!

I wonder if there's a way that Sion could change this strategy to use fewer test spots?

Louis from Prospect House School in England sent in this picture of the grid:

Thank you for sending in this picture, Louis. Can you see where the rectangle will be? The rectangle in this grid is actually a special type of rectangle - what other name do we have for rectangles like this one?

If we didn't have the monkey's clue about how many plugs are used in the rectangle, could we still work out exactly where the rectangle will be using Louis's test spots? Why or why not?

We thought you might also like to see these sketches, drawn by a member of the NRICH team as he was working on a new interactivity for this task:

 

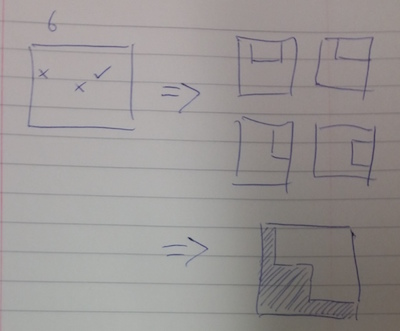
What might he be thinking? 

If you would like to get in touch with us about how you approached this task, please email us with your ideas.